- Objetivos
- Programacion dinámica
- Caminos aleatorios
- Programación estocástica
- Introducción a la programación estocástica
- Cálculo de probabilidades
- Simulación de probabilidades
- Inferencia estadística
- Conclusiones
- Información extra
- Aprender cuándo utilizar Programación Dinámica y sus beneficios.
- Entender la diferencia entre programas deterministas y estocásticos.
- Aprender a utilizar Programacion Estocástica.
- Aprender a crear simulaciones computacionales válidas.
- Aprender a simplificar la notacion big O(n) de ciertos algoritmos de optimización.
La programación dinámica es es un método para reducir el tiempo de ejecución de un algoritmo mediante la utilización de subproblemas superpuestos y subestructuras óptimas.
El matemático Richard Bellman inventó la programación dinámica en 1953 que se utiliza para optimizar problemas complejos que pueden ser discretizados y secuencializados.
La programación dinámica permite optimizar ciertos problemas que cuentan con.
-
Subestructura Óptima: Una solución global óptima se puede encontrar al combinar soluciones óptimas de subproblemas locales.
En otras palabras, los subproblemas se resuelven a su vez dividiéndolos en subproblemas más pequeños hasta que se alcance el caso fácil, donde la solución al problema es trivial.
-
Problemas empalmados:
Una solución óptima que involucra resolver el mismo problema en varias ocasiones (cómo en el caso de la recursiviadad). Es decir, que se usa un mismo subproblema para resolver diferentes problemas mayores. Por ejemplo, en la sucesión de Fibonacci (f3 = f1 + f2) y (f4 = f2 + f3).
La optimizacion para que el programa se ejecute mucho más rápido se logra a través de la memorización:
- La memorización es una técnica para guardar cómputos previos y evitar realizarlos nuevamente.
- Normalmente se utiliza un diccionario { } , donde las consultas se pueden hacer en O(1) .
- Intercambia: Tiempo vs Espacio en memoria.
La memorización nos ayuda a evitar computos adicionales, guardando el resultado de computaciones previas en alguna estructura de datos que podemos consultar rápidamente.
Fun fact : El nombre de Programación Dinámica lo escogió Bellman para esconder a los patrocinadores gubernamentales que financiaban su investigacion, el hecho que en realidad estaba haciendo matemáticas. Lo usó para que ningún congresista pudiera oponerse a financiarlo con ese nombre tan atractivo.
Recordemos los numeros de Fibonacci.
La forma recursiva de Fibonacci f(n) = fn-1 + fn-2 es muy fácil de implementar en código, pero es poco eficiente ya que repetimos el mismo computo muchas veces, aumentando innecesariamente la cantidad de iteraciones y, por lo tanto, el tiempo de ejecución.
Para optimizar esta función haremos uso de la memorización anteriormente mencionada. Aqui tenemos una implementación de Fibonacci Recursivo vs Fibonacci Dinámico:
import sys
def fibonacci_recursivo(n):
if n == 0 or n == 1:
return 1
return fibonacci_recursivo(n-1) + fibonacci_recursivo(n-2)
def fibonacci_dinamico(n, memoria={}):
if n == 0 or n == 1 :
return 1
try:
return memoria[n]
except KeyError:
resultado = fibonacci_dinamico(n-1, memoria) + fibonacci_dinamico(n-2, memoria)
memoria[n] = resultado
return resultado
if __name__ == "__main__":
sys.setrecursionlimit(10000)
n = int(input("Escoge un numero: "))
# resultado = fibonacci_recursivo(n)
resultado = fibonacci_dinamico(n)
print(resultado)def fibonacci_recursivo(n):
if n == 0 or n == 1:
return 1
return fibonacci_recursivo(n-1) + fibonacci_recursivo(n-2)En esta parte tenemos la función de fibonacci_recursivo().
Definimos la función con un parámetro n de entrada, ahora en el primer if cómo sabemos que el caso base de Fibonacci para 0 y 1 es igual a 1 solo retornamos 1.
De no ser así, retornaremos una llamada recursiva de Fibonacci para el numero anterior (n-1) más el numero anterior a ese (n-2).
Recordemos que la recursividad es la forma en la cual se especifica un proceso basado en su propia definición, que en este caso es una función llamandose a sí misma.
def fibonacci_dinamico(n, memoria={}):
if n == 0 or n == 1 :
return 1
try:
return memoria[n]
except KeyError:
resultado = fibonacci_dinamico(n-1, memoria) + fibonacci_dinamico(n-2, memoria)
memoria[n] = resultado
return resultadoAqui tenemos la version dinámica.
Primero definimos la función fibonacci_dinamico(), donde a diferencia de la primera tenemos un parametro extra llamado memoria{} , que es un diccionario que en este caso será nuestra estructura de datos para efectuar la memorización
Ahora tenemos algo nuevo llamado try/except, este es un buen mecanismo para el control del flujo del programa ya que nos permite manejar la excepciones que puedan surgir y tomar acciones de recuperación para evitar la interrupción del programa o, al menos, para realizar algunas acciones adicionales antes de interrumpirlo.
try:
return memoria[n]Dentro del bloque try se ubica todo el código que pueda llegar a levantar una excepción, se utiliza el término levantar para referirse a la acción de generar una excepción.
Si tenemos como llave [n] en el diccionario, regresemos n.
except KeyError:
resultado = fibonacci_dinamico(n-1, memoria) + fibonacci_dinamico(n-2, memoria)
memoria[n] = resultado
return resultadoEl bloque except se encarga de capturar la excepción y nos da la oportunidad de procesarla.
Si NO tenemos como llave [n] en el diccionario, anticiparemos el KeyError que nos saldría al intentar acceder a una llave que no existe.
Nos anticiparemos llamando a la funcion fibonacci_dinamico() para (n-1) y (n-2), pero en este caso tendremos como parametro extra el diccionario memoria{} que es donde guardaremos el resultado anterior para, posteriormente, tomar este valor en la siguiente iteración.
Esta es la parte diferenciadora entre la versión recursiva simple y la versión dinámica, ya que al tener los resultados de iteraciones anteriores dentro del diccionario nos ahorraremos el tiempo del calcular todos los resultados anteriores de n para solo tener que buscar ese resultado anterior dentro del diccionario y sumarlo, lo cual hace MUCHO más eficiente el algoritmo.
Tan solo calcular n=50 con fibonacci_recursivo() toma muchísimo más tiempo que calcular n=500 con fibonacci_dinamico().
import sys
.
.
.
sys.setrecursionlimit(10000)Estas lineas nos ayudan a incrementar el límite de recursividad limitado por python, importando la librería sys para seleccionar el limite de recursión.
NOTA: Hay que tener cuidado con incrementar demasiado el limite de recursividad.
El algoritmo que usa Python internamente para buscar un elemento en un diccionario es muy distinto que el que utiliza para buscar en listas.
Para buscar en las listas, se utiliza un algoritmos de comparación que tarda cada vez más a medida que la lista se hace más larga. En cambio, para buscar en diccionarios se utiliza un algoritmo llamado hash, que se basa en realizar un cálculo numérico sobre la clave del elemento, y tiene una propiedad muy interesante, sin importar cuántos elementos tenga el diccionario, el tiempo de búsqueda es siempre aproximadamente igual O(1).
Este algoritmo de hash es también la razón por la cual las claves de los diccionarios deben ser inmutables, ya que la operación hecha sobre las claves debe dar siempre el mismo resultado, y si se utilizara una variable mutable esto no sería posible.
-
Es un tipo de simulación que elige aleatoriamente una decisión dentro de un conjunto de decisiones válidas.
-
Se utilizan en muchos campos del conocimiento cuando los sistemas no son deterministas e incluyen elementos de aleatoriedad.
-
Nos permiten realizar simulaciones de eventos de carácter probabilístico o no determinista para entender su comportamiento desde otra perspectiva de análisis.
-
Se denomina estocástico al sistema cuyo comportamiento intrínseco es no determinista.
Para este programa imaginemos que queremos describir el comportamiento de un individuo que camina aleatoriamente dando pasos hacia adelante, atras, izquierda y derecha con la misma probabilidad.
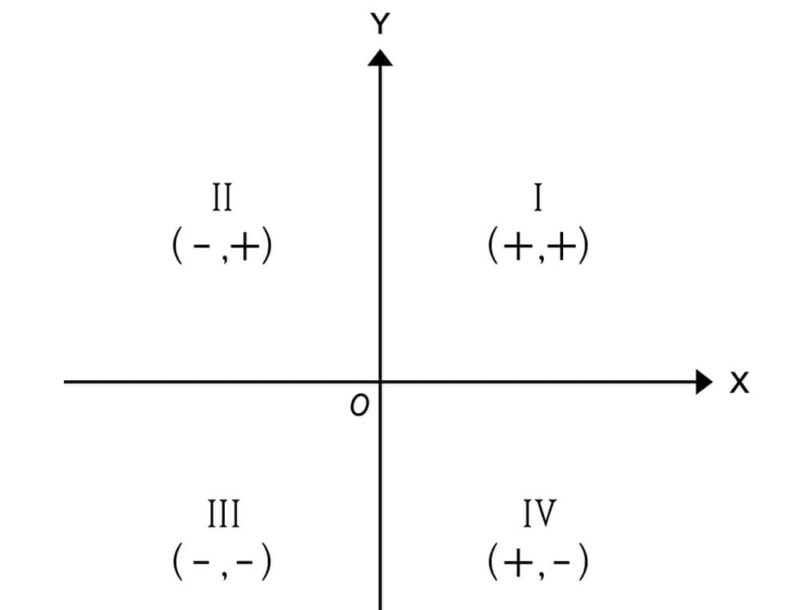
Primero vamos a posicionarnos en un plano cartesiano en donde vamos a describir la trayectoria aleatoria.
Para atacar este problema tomaremos un enfoque de POO, lo vamos a dividir en 3 clases, la clase Individuo que modelará a la persona que efectúa el movimiento, la clase Campo que es el entorno en el cual se va a mover y la clase Coordenada que modelará el punto en el que se encuentra a lo largo del recorrido.
import random
class Individuo:
def __init__ (self,nombre):
self.nombre = nombre
class Aleatorio_Tradicional(Individuo):
def __init__ (self, nombre):
super().__init__(nombre)
def camina(self):
return random.choice([(0,1),(0,-1),(1,0),(-1,0)])Recordando el concepto de herencia de POO, podemos observar que estamos creando la superclase Individuo que solo recibe como parametro nombre (recordemos que self es obligatorio en cada una ya que hace referencia a la instancia).
Después extendemos la superclase Individuo hacia la subclase Aleatorio_Tradicional que modelará una persona que se mueve aleatoriamente con 25% de probabilidad en cada una de las 4 direcciones del plano, en la cual crearemos el método camina() donde gracias al método random.choice simplemente devolverá una selección aleatoria de los valores de nuestra tupla que representa las diferentes direcciones en las que puede dar un paso.
Para la clase Coordenadas tenemos lo siguiente.
class Coordenada:
def __init__(self, x, y):
self.x = x
self.y = y
def mover(self, delta_x, delta_y):
return Coordenada(self.x + delta_x, self.y + delta_y)
def distancia(self, otra_coordenada):
delta_x = self.x - otra_coordenada.x
delta_y = self.y - otra_coordenada.y
return ((delta_x)**2+(delta_y)**2)**0.5 Creamos la clase con parametros x y y en su constructor e iniciamos los atributos de instancia self.x y self.y que almacenarán las coordenadas a lo largo del movimiento.
Después creamos el método mover con parametros delta_x y delta_y el cual se encargará de traer a la clase Coordenada, pero con la siguiente posición, ya que le habrá sumado las diferencias en x y y.
Ahora definimos el método distancia que recibirá como parámetro otra_coordenada, donde tendremos los atributos de instancia delta_x y delta_y las cuales son, respectivamente, las diferencias en en el eje x y y . Despúes efectuaremos el Torema de Pitágoras para obtener la distancia resultante.
En la clase campo tenemos lo siguiente.
class Campo:
def __init__(self):
self.coordenadas_de_persona = {}
def anadir_persona(self, persona, coordenada):
self.coordenadas_de_persona[persona] = coordenada
def mover_persona(self, persona):
delta_x, delta_y = persona.camina()
coordenada_actual = self.coordenadas_de_persona[persona]
nueva_coordenada = coordenada_actual.mover(delta_x, delta_y)
self.coordenadas_de_persona[persona] = nueva_coordenada
def obtener_coordenada(self, persona):
return self.coordenadas_de_persona[persona]Recordemos que el campo modelará el entorno en el que están nuestros individuos y pueden moverse, aquí comenzaremos creando la clase campo que no tendrá más parámetros que la referencia a la instancia y definiremos un artibuto de instancia llamado .coordenadas_de_persona que simplemente sera un diccionario que guardará las coordenadas.
Ahora vamos a crear 3 métodos, el primero será anadir_persona que recibira el parametro persona y coordenda, el cual podemos imaginarlo como la acción se situar a algun individuo en el plano, en cierta coordenada. Aquí mismo tendremos una llamada al atributo .coordenadas_de_persona[persona] que irá guardando las coordenadas en el diccionario que despúes será de ayuda para trazar su recorrido.
El segundo método es mover_persona que tiene como atributo el individuo que queremos mover. Guardaremos en delta_x y delta_y los valores aleatorios arrojados por .camina(), después obtenemos la coordenada actual del diccionario { } del método anterior y ,posteriormente, obtenemos una nueva coordenada que será igual a la coordenada actual más el moviemiento de delta_x y delta_y y esta la añadiremos a nuestra lista de coordenadas.
El tecer método obtener_coordenada solo tendrá como parametro al individuo que queremos ubicar y lo único que hará será regresar el valor de nuestra coordenada almacenada actualmente en nuestra lista de coordenadas.
NOTA: Los tres codigos son archivos independientes.
Lo siguiente será desarollar el programa que se encargue de la simulación.
from individuo import Aleatorio_Tradicional
from campo import Campo
from coordenada import Coordenada
def caminata(campo, persona, pasos):
inicio = campo.obtener_coordenada(persona)
for _ in range(pasos):
campo.mover_persona(persona)
return inicio.distancia(campo.obtener_coordenada(persona))
def simular_caminata(pasos, numero_de_intentos, tipo_de_tendencia):
persona = tipo_de_tendencia(nombre='Nombre1')
origen = Coordenada(0,0)
distancias = []
for _ in range(numero_de_intentos):
campo = Campo()
campo.anadir_persona(persona, origen)
simulacion_caminata = caminata(campo, persona, pasos)
distancias.append(round(simulacion_caminata, 1))
return distancias
def main(distancias_de_caminata, numero_de_intentos, tipo_de_tendencia):
for pasos in distancias_de_caminata:
distancias = simular_caminata(pasos, numero_de_intentos, tipo_de_tendencia)
distancia_media = round(sum(distancias) / len(distancias), 4)
distancia_maxima = max(distancias)
distancia_minima = min(distancias)
print(f'{tipo_de_tendencia.__name__} caminata aleatoria de {pasos} pasos')
print(f'Media = {distancia_media}')
print(f'Distancia maxima = {distancia_maxima}')
print(f'Distancia minima = {distancia_minima}')
if __name__ == '__main__':
distancias_de_caminata = [10,100,1000,10000]
numero_de_intentos = 100
main(distancias_de_caminata, numero_de_intentos, Aleatorio_Tradicional) from individuo import Aleatorio_Tradicional
from campo import Campo
from coordenada import CoordenadaLa primera seccion se encargara de importar las clases Aleatorio_Tradicional, Campo y Coordenada de sus módulos correspondientes.
Primero crearemos nuestra función caminata() para simular el comportamiento de moverse en el plano.
def caminata(campo, persona, pasos):
inicio = campo.obtener_coordenada(persona)
for _ in range(pasos):
campo.mover_persona(persona)
return inicio.distancia(campo.obtener_coordenada(persona))Tendremos como parámetros campo, persona y pasos para deescribir el movimiento en el plano. Y pasamos a crear una variable que nos de el punto inicial de cada movimiento que lo que hará será ejecutar el método de Campo obtener_coordenada().
Creamos un ciclo for _ donde no tenemos variable i, eso significa que solo crearemos el rango que será el número de pasos que dé la persona en la simulación. Y en cada iteración o paso vamos a ejecutar el método de Campo .mover_persona y después obtenemos la distancia que hay entre la coordenada de inicio y la otra coordenada con .distancia, método definido en el módulo de coordenada.
Después crearemos la función simular_caminata() .
def simular_caminata(pasos, numero_de_intentos, tipo_de_tendencia):
persona = tipo_de_tendencia(nombre = 'Abdiel')
origen = Coordenada(0,0)
distancias = []
for _ in range(numero_de_intentos):
campo = Campo()
campo.anadir_persona(persona, origen)
simulacion_caminata = caminata(campo, persona, pasos)
distancias.append(round(simulacion_caminata, 1))
return distanciasPara esta función nos interesa saber cuantos pasos dio el individuo, el número de veces que se ejecutó la simulación y la subclase a la que nos referimos.
Vamos a crear una variable llamada persona que va a inicializar una instancia de la subclase. Despúes definimos el origen de coordenadas (0,0) y creamos una lista[ ] donde guardaremos los valores de las distancias que obtengamos en cada una de la simulaciones. Ejecutaremos un ciclo for() para un rango que en este caso es el numero_de_intentos de la simulación.
Posteriormente se ejecutara un bloque de instrucciones donde primero haremos una llamada a la clase Campo() y ejecutaremos el método de Campo .anadir_persona para posicionarla en el punto inicial de nuestra simulación. Posteriormente guardamos en la variable simulacion_caminata el valor arrojado al ejecutar la funcion caminata() anteriormente añadida, después agregamos ese valor a nuestra lista de distancias y recortamos los decimales. Y finalmente retornamos nuestro valor de distancias.
El siguiente paso será definir main() con las funciones que queremos que se ejecuten.
def main(distancias_de_caminata, numero_de_intentos, tipo_de_tendencia):
for pasos in distancias_de_caminata:
distancias = simular_caminata(pasos, numero_de_intentos, tipo_de_tendencia)
distancia_media = round(sum(distancias) / len(distancias), 4)
distancia_maxima = max(distancias)
distancia_minima = min(distancias)
print(f'{tipo_de_tendencia.__name__} caminata aleatoria de {pasos} pasos')
print(f'Media = {distancia_media}')
print(f'Distancia maxima = {distancia_maxima}')
print(f'Distancia minima = {distancia_minima}')Nuestra funcion principal main() tendra como parámetros la cantidad de pasos, el número de veces que se correrá la simulación, y la clase que utilizaremos.
Ahora, creamos un for para ejecute el siguiente bloque de instrucciones mientras aumenta una variable iteradora pasos que representará la cantidad de pasos que dará el individuo en la simulación. Dentro de ese bloque de código creamos la variable distancias que hará una llamada a una funcion simular_caminata() y guardará el valor arrojado por ella.
Recordemos que se efectuara varias veces caminata() por lo que tendremos diferentes datos y lo que nos interesa son los valores medio, máximo y mínimo de las distancias. Las siguiente instrucciones son para obtener e impimir esos valores deseados usando funciones ya conocidas como max(), min() y una simple media aritmética redondeada a 3 decimales.
En nuestro entry point tenemos lo siguiente.
if __name__ == '__main__':
distancias_de_caminata = [10,100,1000,10000]
numero_de_intentos = 100
main(distancias_de_caminata, numero_de_intentos, Aleatorio_Tradicional) Siempre que hagamos un programa de POO debemos de definir nuestra función main(), ya que será el punto de entrada donde definimos que harán nuestros objetos.
Aquí es donde definimos la cantidad de pasos que queremos que el individuo efectúe en la simulación y podemos ver que definimos una lista[ ] de valores para tener una cantidad considerable de datos. Lo siguiente es definir cuantas veces vamos a ejecutar nuestra simulación que en este caso es de 100.
Y ejecutamos el main() que es donde establecimos los datos que queremos que reciba nuestra simulación que en este caso serán la cantidad de pasos, el número de intentos de la simulación y la subclase Aleatorio_Tradicional junto con todo el bloque de intrucciones que escribimos dentro de la función.
Usaremos bokeh para nuestra simulación, recordemos que para incluir la libreria en nuestro programa tenemos que generar nuestro ambiente virtual.
Ejecutaremos la siguiente instruccion en la terminal en la dirección donde esta nuestro programa:
py -m venv env
env\Scripts\activate.bat
pip install boke
Ahora ya tendremos instalado nuestro paquete no a nivel global sino solo en el área que lo queremos.
En nuestro archivo principal de caminata_aleatoria.py agregaremos la linea de código:
from bokeh.plotting import figure, show
Que, según la documentación de bokeh, bokeh.plotting creará una nueva figura para graficar, la subclase de Plot simplifica la gráfica con ejes, cuadriculas y herramientas que trae por default. Mientras que show se encarga de mostrar los resutlados.
Ahora vamos a añadir una pequeña función que nos ayudará a graficar:
def graficar(x,y):
grafica = figure(title = 'Caminata aleatoria', x_axis_label = 'pasos', y_axis_label = 'distancias')
grafica.line(x, y, legend = 'Distancia media')
show(grafica)Sabemos que si queremos trazar una linea depende de dos parámetros (x,y), con figure() nos vamos a encargar de ponerle nombre a las etiquetas del gráfico y de los ejes x y y. Con grafica.line() hacemos una llamada al método line() de figure que nos facilitará el trazado de la linea y finalmente con show() lo que haremos será mostrar el resultado.
Y en el main() agregaremos lo datos que requiere nuesta funcion graficar() añadida anteriormente:
distancias_media_por_caminata = []
for pasos in distancias_de_caminata:
.
.
.
distancias_media_por_caminata.append(distancia_media)
graficar(distancias_de_caminata, distancias_media_por_caminata)Generamos la variable distancias_media_por_caminata que guardará en una lista los valores de distancia_media arrojados en cada iteración dentro del ciclo for para posteriormente hacer una llamada a la función graficar() pasando como parámetros x y y las distancias_de_caminata y distancias_media_por_caminata respetivamente.
Para evitar confusión recordemos que
-
distancias_de_caminata: Es igual a la lista de valores [10,100,1000,10000] que representa el número de pasos que dará el indiviuo. -
distancias_media_por_caminata: Representa la distancia media arrojada por nuestro ciclo for.
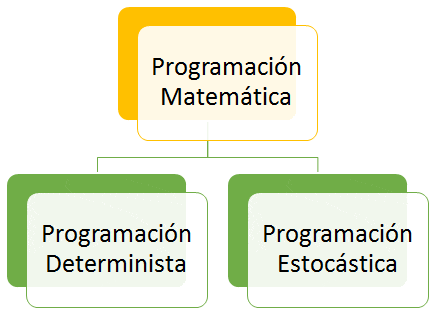
- La Programación Estocástica reúne aquellos modelos de optimización en donde uno o más parámetros del problema son modelados a través de variables aleatorias.
- Un programa es NO determinísta si cuando se corre el mismo input NO produce el mismo output.
- Existen problemas que no pueden resolverse con un programa determinístico y por ello requerimos ciertas implementaciones de programación estocástica.
- La programación estocástica se aprovecha si conocemos las distribuciones de probabilidad del problema planteado o si podemos estimarlas.
Los modelos de optimización estocástica se dividen en dos grandes categorías, por un lado tenemos Modelos con Restricciones Probabilísticas y por otro Modelos con recurso.
- La probabilidad es una medida de la certidumbre asociada a un evento, y suele expresarse con un número entre 0 y 1.
- Una probabilidad de 0 significa que sabemos que jamás sucederá.
- Una probabilidad de 1 significa que esta garantizado que un evento ocurrirá.
Ley del complemento
Regla de multiplicación
Regla de adición
Por otro lado:
Vamos a generar una simulación de un lanzamiento de dados.
Para este tipo de simulaciones tengamos presente la ley de los grandes números, donde se engloban varios teoremas que describen el comportamiento del promedio de una sucesión de variables aleatorias conforme aumenta su número de ensayos.
Las leyes de los grandes números explican por qué el promedio de una muestra al azar de una población de gran tamaño tenderá a estar cerca de la media de la población completa.
import random
def tirar_dado(numero_de_intentos):
secuencia_de_tiros = []
for _ in range(numero_de_tiros):
tiro = random.choice([1,2,3,4,5,6])
secuencia_de_tiros.append(tiro)
return secuencia_de_tiros
def main(numero_de_tiros, numero_de_intentos):
tiros = [] #En este arreglo guardaremos los datos de los tiros.
for _ in range(numero_de_intentos):
secuencia_de_tiros = tirar_dado(numero_de_tiros)
tiros.append(secuencia_de_tiros)
tiros_con_1 = 0
for tiro in tiros:
if 1 in tiro:
tiros_con_1 += 1
probabilidad_de_tiros_con_1 = tiros_con_1 / numero_de_intentos
print(f'Probabilidad de obtener POR LO MENOS un 1 en {numero_de_tiros} tiros = {probabilidad_de_tiros_con_1}')
if __name__ == '__main__':
numero_de_tiros = int(input('Cuantas veces se va a tirar el dado?: '))
numero_de_intentos = int(input('Cuantas veces se va a correr la simulación?: '))
main(numero_de_tiros, numero_de_intentos)

Podemos ver que mientras aumentamos la cantidad de veces que corremos la simulación podemos aproximarnos cada vez más al valor real 0.1666 a pesar de que en cada simulación tengamos 1 solo lanzamiento.
- Con las simulaciones podemos calcular las probabilidades de eventos complejos sabiendo las probabilidades de eventos simples.
- ¿Qué pasa cuando no sabemos las probabilidades de los eventos simples?
- La técnicas de la inferencia estadística nos permiten intefir/concluir propiedades de una población a partir de una muestra aleatoria.
El principio guía de la inferencia estadística es que una muestra aleatoria tiende a exhibir las mismas propiedades que la poblacion de la cual fue extraída.
Recordemos la Ley fuerte de los grandes números.
En pruebas indepentientes repetidas con la misma probabilidad P de un resultado, la fracción de desviaciones de P converge a cero conforme la cantidad de pruebas se acerca al infinito.
La ley fuerte de los grandes números establece que si X1, X2, X3, ... es una sucesión infinita de variables aleatorias independientes e idénticamente distribuidas que cumplen E(|Xi|) < ∞ y tienen el valor esperado μ, entonces:
es decir que, que conforme las muestras tienden a infinito, la probabilidad de que la media de la muestra sea igual a la media de la población es 1.Esto nos da la oportunidad de que al tener una población de una grán cantidad de datos de los cuales queremos extraer información estadística, basta con extraer una muestra aleatoria y hacer inferencias sobre ella.
Grandes números de individuos, actuando independientemente en un sistema, producen regularidades que no dependen de su coordinacion mutua, de manera que es posible razonar sobre la colectividad sin ningún conocimiento detallado de los individuos. -‘Simeon Denis Poisson’
La falacia del apostador consiste en creer que un evento aleatorio pasado condiciona un evento aleatorio futuro. Y a pesar de que parece un razonamiento bastante intuitivo resulta que el la practica podemos caer en la falacia.
Por ejemplo al creer que:
- Al ocurrir un evento extremo tendrá que ocurrir un evento menos extremo para nivelar la media.
Cuando en realidad:
- La regresión a la media señala que después de ocurrir un evento aleatorio extremo, el siguiente evento probablemente será menos extremo.
- Es una medida de tendencia central.
- Comúnmente es conocida como el promedio.
- La media muestral se define como:
NOTA: La media poblacional se de denota por: µ A continuacion un pequeño programa para calcular la media de una lista de 20 valores aleatorios:
import random
def media(X):
return sum(X) / len(X)
if __name__ == '__main__':
X = [random.randint(1,21) for i in range(20)]
µ = media(X)
print(X)
print(µ)- La varianza mide qué tan propagados se encuentran un conjunto de valores aleatorios de su media.
- Mientras que en la media nos da una idea de donde se encuentran los valores, la varianza nos dice que tan dispersos se encuentran esos datos.
- La varianza siempre debe entenderse con respecto a la media.
- La desviación estándar es la raíz cuadrada de la varíanza.
- Nos permite entender, tambíen, la propagación relativa con la media.
- La ventaja sobre la varianza es que la desviación estándar está en las mismas unidades que la media (No está al cuadrado).
Veamos como implementar la varianza para variables aleatorias discretas.
import random
import math
def media(X):
return sum(X) / len(X)
def varianza(X):
mu = media(X)
contador = 0
for x in X:
contador += (x - mu)**2
return contador / len(X)
def desviacion_estandar(X):
return math.sqrt(varianza(X))
if __name__ == '__main__':
X = [random.randint(1,2) for i in range(20)]
mu = media(X)
var = varianza(X)
sigma = desviacion_estandar(X)
print(f'\nValores random:\n{X}\n')
print(f'Media: {mu}\n')
print(f'Varianza: {round(var,3)}\n')
print(f'Desviación estándar: {round(sigma,3)}\n')-
Es una de las distribuciones más recurrentes en cualquier ámbito.
-
Se define completamente por su media y su desviación estándar.
-
Permite calcular intervalos de confianza con la regla empírica.
-
También conocida como la regla 68-95-99.7.
-
Señala cuál es la dispersión de los datos en una distribución normal a uno, dos y tres sigmas.
-
Permite calcular probabilidades con la densidad de la distribución normal.
- Permite crear simulaciones para predecir el resultado de un problema.
- Permite convertir problemas determinísticos en problemas estocásticos.
- Es utilizado en una gran diversidad de áreas, desde la ingeniería hasta la biología y el derecho.
Un pequeño programa para calcular la probabilidad de obtener un color o corrida
import random
import collections
def crear_baraja():
NEGRAS = ['Picas','Treboles']
ROJAS = ['Corazones','Diamantes']
NUMEROS = ['A','2','3','4','5','6','7','8','9','10','J','Q','K']
baraja = []
for i in NEGRAS:
for j in NUMEROS:
baraja.append((i,j))
for i in ROJAS:
for j in NUMEROS:
baraja.append((i,j))
return baraja
#print(baraja)
def tomar_una_mano(tamano_de_mano):
baraja = crear_baraja()
mano = random.sample(baraja, tamano_de_mano)
return mano
def main(tamano, intentos):
baraja = crear_baraja()#Llamamos a la creación de las cartas
manos = []
for _ in range (int(intentos)):#Por cada intento tomaremos n cartas
mano = tomar_una_mano(tamano)
#print(f'\n {mano}')
manos.append(mano)
#print(f'\n {manos}\n')
corrida = 0
for i in manos:
valores = []
for j in i:
valores.append(j[0])
#print(valores)
contador = dict(collections.Counter(valores))#Cuenta cuantas veces aparece un valor por cada ejecución
#print(contador)
for i in contador.values():##Usamos values por que cualquiera que tenga 5 cartas del
#mismo palo es una corrida. De querer obtener un valor en concreto usariamos el
#valor contenido en el contador y no el cuantas veces aparece.
if i == 5:
corrida += 1
probabilidad_corrida = corrida / intentos
print(f'La probabilidad de una corrida es de: {probabilidad_corrida}')
if __name__ == '__main__':
tamano = int(input('Ingrese el tamaño de la mano: '))
intentos_simulacion = int(input('Cuantas veces se ejecutará la simulación?:'))
main(tamano, intentos_simulacion)¿Cómo podemos cálcular pi con aleatoriedad?
Imaginemos un circulo unitario iscrito en un cuadrado de 2x2. De esta forma tendremos un cuadrado con área = 4 y un circulo de área = Pi
Ahora, imaginemos que lanzamos aleatoriamente unos puntitos dentro del cuadrado, de manera de que todos queden dentro del cuadrado, pero solo algunos dentro del circulo. Al hacer esto existirá una proporción entre los puntitos dentro del circulo y dentro de todo el cuadrado (por tratarse de un subconjunto de los puntitos dentro del cuadrado).
Tendremos que la relación de puntitos en el circulo respecto a los puntitos del cuadrado sera igual a la proporción existente entre las areas del círculo y el área del cuadrado.
Y como en este caso tenemos que r =1, podremos despejar la ecuación anterior y obtener que pi será igual a el numero de puntos dentro del circulo por el área del cuadrado entre el numero de puntos totales (puntos dentro del cuadrado).
¿Y cómo sabremos que un punto estuvo dentro del circulo?
Sabemos que el circulo tiene radio r=1 por lo que podemos calcular la distancia de un punto al origen de coordenadas utilzando teorema de pitágoras teniendo los 2 casos en que:
- El radio r <= 1 entonces esta dentro del círculo.
- El radio r > 1 entonces esta fuera del círculo.
Obviamente teniendo en cuenta que TODOS los puntos tienen que estar si o si dentro del cuadrado, ya que de ahi obtuvimos nuestra realción de las proporciones.
Veamos la implementación en código
import random
import math
from funciones_estadisticas import desviacion_estandar, media
#De nuestro programa anterior importamos estas funciones que son de utilidad.
def lanzar_puntitos(total_de_puntitos):
adentro_circulo = 0 #Inicialmente no hay ninguno
for _ in range(total_de_puntitos):
x = random.random() * random.choice([-1,1])
y= random.random() * random.choice([-1,1])
#Originalmente arroja un valor entre 0 y 1
#Por ello lo multiplicamos por -1 o 1 aleatoriamente para tener
#el rango de puntos dentro del cuadrado.
pitagorazo = math.sqrt(x**2 + y**2)
if pitagorazo <= 1:
adentro_circulo += 1
return (4 * adentro_circulo) / (total_de_puntitos)
#Recordemos que el 4 representa el area de nuestro cuadrado de 2x2
def estimacion(total_de_puntitos, intentos):
estimados = []
for _ in range (intentos):
estimacion_pi = lanzar_puntitos(total_de_puntitos)
estimados.append(estimacion_pi)
media_estimados = media(estimados)
sigma = desviacion_estandar(estimados)
print(f'Estimado = {round(media_estimados , 5)}, desviación estándar = {round(sigma , 5)} de un total de {total_de_puntitos} lanzamientos.')
return (media_estimados, sigma)
def estimar_pi(precision, numero_de_intentos):
numero_de_puntitos = 10000
sigma = precision
while sigma >= precision / 1.96:
#95% de confiabilidad
media, sigma = estimacion(numero_de_puntitos, numero_de_intentos)
numero_de_puntitos *= 2
return media
if __name__ == '__main__':
estimar_pi(0.01, 100)Si ejecutamos el programa podremos darnos cuenta que a medida que ejecutamos más y más veces con más puntos nuestra desviación estándar ira disminuyendo, pero a pesar de ello el valor obtenido en algunos casos comenzara a alejarse del valor real de pi.
Esto ocurre por que estamos obteniendo un resultado estádistico cada vez más certero según el método de inferencia estádistica que estemos empleando, y esto no tiene necesariamente que coincidir con la axactitud del valor real ya que este tambien dependerá de que tan bueno sea nuestro algoritmo, que tan buena sea la aproximación que tengamos y que tipo de tecnicas de inferencia estamos utilizando.
Aquí tenemos una diferencia entre una respuesta estadisticamente válida y una respuesta válida.
-
Hay ocasiones en las que no tenemos acceso a toda la población que queremos explorar.
-
Uno de los grandes descubrimientos de la estadística es que, las meustras aleatorias tienen a mostrar las mismas propiedades de la población objetivo.
-
El tipo de muestreo que hemos hecho hasta ahora es muestreo probabilístico.
-
En un muestreo aleatorio cualquier miembtro de la población tiene la misma probabilidad de ser escogido.
-
En un muestreo estratificado tomamos en consideración las características de la población para partirla en subgrupos o subconjuntos de ella y luego tomamos muestras de cada uno de esos subgrupos.
- Esto incrementa la probabilidad de que el muestreo sea representativo de la población.
- Nos ayuda a evitar sesgos.
-
Es uno de los teoremas más importantes de la estadística.
-
Establece que muestras aleatorias de cualquier distribución van a tener una distribución normal (la distribución de las medias de las muestras tiende a ser una distribución normal).
-
Mientras aumentamos la cantidad de muestras aumentamos la aproximación hacia una distribución normal.
-
Permite entender cualquier distribución como la distribución normal de sus medias y eso nos permite aplicar todo lo que ya sabemos de distribuciones normales (ademas de ser más intuitiva al analizar el problema con esa distribución).
-
Es la aplicación del método científico.
-
Es necesario comenzar con una teoría o hipótesis sobre el resultado al que se quiere llegar.
-
Basado en la hipótesis se debe crear un experimento para validar o flasear la hipótesis.
-
Se valida o falsea una hipótesis midiendo la diferencia entre las mediciones experimentales y aquellas mediciones predichas por la hipótesis.
-
Permite aproximar una función a un conjunto de datos obtenidos de manera experimental.
-
No necesariamente permite aproximar funciones lineales, sino que sus variantes permiten aproximar cualquier función polinómica.
A continuación estaremos trabajando con algunas librerias un poco más avanzadas y muchas veces requerimos instalarlas desde conda, pero para esta ocasión usaremos un ambiente distinto que ya tiene incorporadas las librerias necesarias; usaremos Google Colab que es una implementación de JupyterNotebooks.
import numpy as np #Importamos la libreria
x = np.array([0,1,2,3,4,5,6,7,8])#Convierte una lista en vectores
#Introducimos los valores de la variable independiente del experimento
y = np.array([1,2,3,5,4,6,8,7,9])#Los resultados del experimento
coeffs = np.polyfit(x, y, 1)#Obtenemos nuestros coeficientes
print(coeffs)
a = coeffs[0]
b = coeffs[1]
estimado_y = (a*x) + b #Formamos una recta
import matplotlib.pyplot as plt
plt.plot(x, estimado_y)
plt.scatter(x, y)
plt.show()Algunas libreria para la visualización en python son:
- Bokhe
- Mathplitlib
- Seaborn
- ploty
- Altair
- La programación dinámica permite optimizar problemas que tienen subestructura óptima y subproblemas empalmados.
- Las computadoras pueden resolver problemas determinísticos y estocásticos.
- Podemos generar simulaciones computacionales para responder preguntas del mundo real.
- La interferencia estadística nos permite tener confianza de que nuestras simulaciones arrojan resulados válidos.
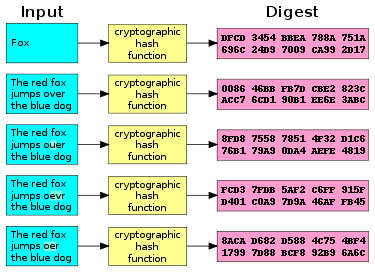
Es un algoritmo matemático que transforma cualquier bloque arbitrario de datos en una nueva serie de caracteres con una longitud fija. Para la creación de un hash se toman los datos sin importar el tamaño de estos, y en base a ellos creamos un identificador único.
Por ejemplo:
Hola, este mensaje se codifico usando MD5 Mensaje
bb670be8836c9e5e8300732dbcf05380 HASH generado
hola, este mensaje se codifico usando MD5 Mensaje
022a8ca36703e0269596b57d902e3a44 HASH generado
Podemos ver que al cambiar la primera letra H por una h el hash ha cambiado por completo, de aqui la magía de utilizar esta función. De hecho, son muy usados en el procedimiento del minado de criptoactivos como el bitcoin, especialmente en el método de generación de los bloques del blockchain.
Si tu conoces la fórmula o expresion matemática para generarlo es muy facíl obtener el HASH a partir del dato, pero teniendo solo el HASH es muy dificíl y casi imposible dependiendo del protocolo usado, obtener el dato original.
Cabe aclarar que al no contar con llaves, cómo por ejemplo en el protocolo SSH, no cuenta como un algoritmo de cifrado.
Las funciones de HASH son muy usadas en seguridad y criptografía, por ejemplo en el proceso de validación de la autentificación de usuarios, almacenamiento de contraseñas con protocolos de seguridad como PBDKF2 que dificulta recuperar las contraseñas en el caso de un ataque.
El uso de HASHes nos brinda:
- Unidireccionalidad: Hace computacionalmente imposible revertir el proceso y obtener la información previa al algoritmo.
- Compresión: Suponiendo que la información contenida tiene M bits y el HASH una longitud de N bits con M > N , podemos trabajar con una menor longitud de bits al autentificar la información a través del HASH.
- Facilidad de cálculo: Los algoritmos de hash son muy eficientes y no requieren grandes potencias de cálculo para ejecutarse ya que tendremos un O(M).
- Difusión de bits o efecto de avalancha: Como mencionamos en el ejemplo, al modificar un solo bit del mensaje se modifica por completo el HASH obtendio (aproximadamente en la mitad de bits respecto al anterior).