This Julia package implements a two-dimensional plane-based geometric algebra on top of CliffordAlgebras.jl. The multivectors of the algebra can encode points, lines, directions and motors. This package provides a number of named operations on these objects to make using the algebra easier and more intuitive. In addition, we also offer a Plots.jl recipe for visualising the supported geometric primitives.
Create points, lines and directions.
julia> using PGA2D
julia> point(0,0)
point(0.0, 0.0) ≜ +1×e1e2 ∈ Cl(2, 0, 1)
julia> line(1,1,0)
line(0.7071067811865475, 0.7071067811865475, 0.0) ≜ +1×e1+1×e2 ∈ Cl(2, 0, 1)
julia> direction(2,1)
direction(2, 1) ≜ +1×e0e1+2×e2e0 ∈ Cl(2, 0, 1)
Line coordinates are given as the coefficients (a,b,c) in the line equation a x + b y + c = 0. Coordinates can be extracted from MultiVectors:
julia> point_coordinates(point(-2,1))
(-2.0, 1.0)
julia> line_coordinates(line(-1,1,-3))
(-1, 1, -3)
julia> direction_coordinates(direction(1,0))
(1, 0)
However, if the MultiVector does not encode the object we are asking for, we will receive a DomainError:
julia> direction_coordinates(line(-1,1,-3))
ERROR: DomainError with line(-0.7071067811865475, 0.7071067811865475, -2.1213203435596424) ≜ -1×e1+1×e2-3×e0 ∈ Cl(2, 0, 1):
is not a direction.
We can make sure we have the right kind of object by using the following methods:
julia> p = point(2,1)
point(2.0, 1.0) ≜ +1×e1e2+1×e0e1+2×e2e0 ∈ Cl(2, 0, 1)
julia> is_point(p)
true
julia> is_line(p)
false
julia> is_direction(p)
false
If you would like to work with the MultiVectors directly, you can use the exported symbols pga2d for the global algebra instance and PGA2DMV for the MultiVector type. The basis vectors for Clifford(2,0,1) are also exported as e0, e1, e2, e01, e12, e20, e012 or alternatively 𝐈. For full support of the underlying Clifford Algebra, you can import CliffordAlgebras.
The recommended use of this package is to rely on the available higher-level functions that act on points, directions and lines. Because the type of all objects is that of the MultiVector PGA2DMV, the geometric functions can not check for the proper type. You can provide a line in place of a point and get a MultiVector as a result. To make sure you are aware of the expected object, the nomenclature of the functions is designed to indicate both the kind of object returned and the expected argument types.
The function l_ortho_lp returns a line, as indicated by the leading l. The line is orthogonal to the line and passes through the point provided as arguments and described by the lp suffix:
julia> p = point(1,1)
point(1.0, 1.0) ≜ +1×e1e2+1×e0e1+1×e2e0 ∈ Cl(2, 0, 1)
julia> l = line(1,1,0)
line(0.7071067811865475, 0.7071067811865475, 0.0) ≜ +1×e1+1×e2 ∈ Cl(2, 0, 1)
julia> l_ortho_lp(l,p)
line(-0.7071067811865475, 0.7071067811865475, 0.0) ≜ -1×e1+1×e2 ∈ Cl(2, 0, 1)
There are many more functions that allow us to intersect two lines, find the line passing through to two points, find distances and angles, bisect angles and distances, calculate areas and transform objects using motors. Functions that are missing should be easily composable from the functions in this package.
The two-dimensional plane-based geometric algebra can be used for 2D constructive geometry with lines and points. The package Constructions.jl provides the necessary framework for such constructions.
Let's construct a triangle:
julia> using PGA2D, Constructions, Plots
julia> plotly()
julia> C = Construction()
julia> @place C "P1" point(0,0)
point(0.0, 0.0) ≜ +1×e1e2 ∈ Cl(2, 0, 1)
julia> @place C "P2" point(1,0)
point(1.0, 0.0) ≜ +1×e1e2+1×e2e0 ∈ Cl(2, 0, 1)
julia> @place C "P3" point(0,1)
point(0.0, 1.0) ≜ +1×e1e2+1×e0e1 ∈ Cl(2, 0, 1)
julia> @construct C "L12" join_pp "P1" "P2"
line(0.0, 1.0, 0.0) ≜ +1×e2 ∈ Cl(2, 0, 1)
julia> @construct C "L13" join_pp "P1" "P3"
line(-1.0, 0.0, 0.0) ≜ -1×e1 ∈ Cl(2, 0, 1)
julia> @construct C "L23" join_pp "P2" "P3"
line(-0.7071067811865475, -0.7071067811865475, 0.7071067811865475) ≜ -1×e1-1×e2+1×e0 ∈ Cl(2, 0, 1)
julia> plot(C ; aspect_ratio = :equal)
Now we can construct the perimeter center point ...
julia> @construct C "Lb12" l_bisect_pp "P1" "P2"
line(1.0, -0.0, -0.5) ≜ +2.0×e1-1.0×e0 ∈ Cl(2, 0, 1)
julia> @construct C "Lb23" l_bisect_pp "P2" "P3"
line(-0.7071067811865475, 0.7071067811865475, 0.0) ≜ -2.0×e1+2.0×e2 ∈ Cl(2, 0, 1)
julia> @construct C "Pcirc" meet_ll "Lb12" "Lb23"
point(0.5, 0.5) ≜ +4.0×e1e2+2.0×e0e1+2.0×e2e0 ∈ Cl(2, 0, 1)
... and the center of gravity:
julia> @construct C "Lb1" (l1,l2)->l_bisect_ll(l1,l2)[1] "L12" "L13"
line(-0.7071067811865475, 0.7071067811865475, 0.0) ≜ -1.0×e1+1.0×e2 ∈ Cl(2, 0, 1)
julia> @construct C "Lb2" (l1,l2)->l_bisect_ll(l1,l2)[2] "L12" "L23"
line(0.4472135954999579, 0.8944271909999159, -0.4472135954999579) ≜ +0.7071067811865475×e1+1.414213562373095×e2-0.7071067811865475×e0 ∈ Cl(2, 0, 1)
julia> @construct C "Pcog" meet_ll "Lb1" "Lb2"
point(0.3333333333333333, 0.3333333333333333) ≜ -2.1213203435596424×e1e2-0.7071067811865475×e0e1-0.7071067811865475×e2e0 ∈ Cl(2, 0, 1)
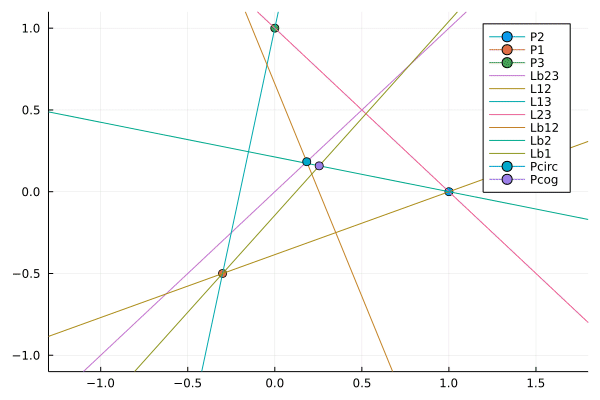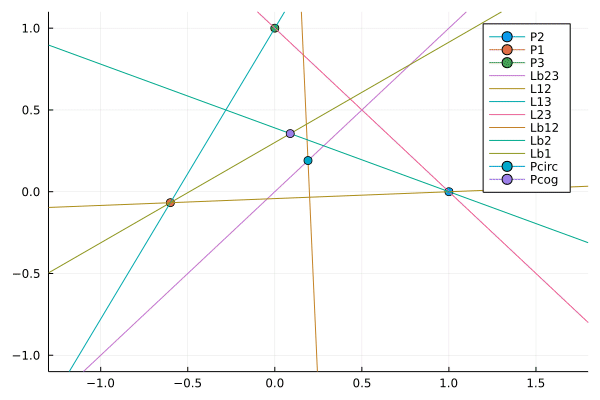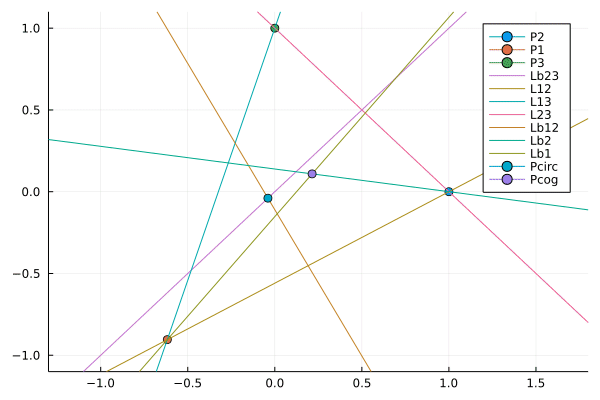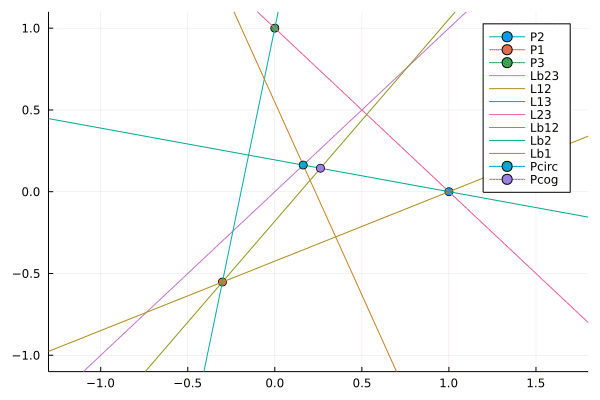
Plotting the result shows our work so far:
julia> plot(C ; aspect_ratio = :equal)
The construction object C has stored all the rules required for the construction:
julia> C
P2: point(1.0, 0.0) ≜ +1×e1e2+1×e2e0 ∈ Cl(2, 0, 1);
P1: point(0.0, 0.0) ≜ +1×e1e2 ∈ Cl(2, 0, 1);
P3: point(0.0, 1.0) ≜ +1×e1e2+1×e0e1 ∈ Cl(2, 0, 1);
{P2, P3, } => Lb23: line(-0.7071067811865475, 0.7071067811865475, 0.0) ≜ -2.0×e1+2.0×e2 ∈ Cl(2, 0, 1);
{P2, P1, } => L12: line(0.0, 1.0, 0.0) ≜ +1×e2 ∈ Cl(2, 0, 1);
{P1, P3, } => L13: line(-1.0, 0.0, 0.0) ≜ -1×e1 ∈ Cl(2, 0, 1);
{P2, P3, } => L23: line(-0.7071067811865475, -0.7071067811865475, 0.7071067811865475) ≜ -1×e1-1×e2+1×e0 ∈ Cl(2, 0, 1);
{P2, P1, } => Lb12: line(1.0, -0.0, -0.5) ≜ +2.0×e1-1.0×e0 ∈ Cl(2, 0, 1);
{L12, L23, } => Lb2: line(0.4472135954999579, 0.8944271909999159, -0.4472135954999579) ≜ +0.7071067811865475×e1+1.414213562373095×e2-0.7071067811865475×e0 ∈ Cl(2, 0, 1);
{L12, L13, } => Lb1: line(-0.7071067811865475, 0.7071067811865475, 0.0) ≜ -1.0×e1+1.0×e2 ∈ Cl(2, 0, 1);
{Lb23, Lb12, } => Pcirc: point(0.5, 0.5) ≜ +4.0×e1e2+2.0×e0e1+2.0×e2e0 ∈ Cl(2, 0, 1);
{Lb1, Lb2, } => Pcog: point(0.3333333333333333, 0.3333333333333333) ≜ -2.1213203435596424×e1e2-0.7071067811865475×e0e1-0.7071067811865475×e2e0 ∈ Cl(2, 0, 1);
We can see that the points P1, P2 and P3 that have been inserted with @place do not have any dependencies, but they do appear as dependencies of other geometric elements. We can modify these points and the entire construction will update:
julia> @modify C "P1" point(0.25,-0.5)
point(0.25, -0.5) ≜ +1.0×e1e2-0.5×e0e1+0.25×e2e0 ∈ Cl(2, 0, 1)
julia> plot(C ; aspect_ratio = :equal)
We can also create an animation to show how the construction adapts to changes:
julia> gr()
Plots.GRBackend()
julia> pl = plot()
julia> @gif for x = 0:59
@modify C "P1" point(-0.5+0.2*cos(2*pi*x/60), -0.5+0.5*sin(2*pi*x/60))
plot(pl, C, xlims = (-1.3,1.8), ylims = (-1.1,1.1) )
end
For a more detailed discussion of the capabilities of Constructions.jl please see the package website.