Skip to content

Latest commit

 

History

History
1249 lines (913 loc) · 83.6 KB

Tree-based and Ensemble methods.md

File metadata and controls

1249 lines (913 loc) · 83.6 KB
Raw

Tree-based Learning Algorithms

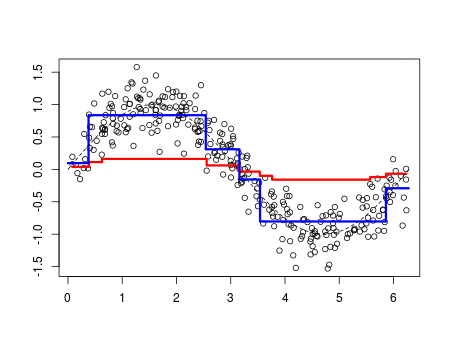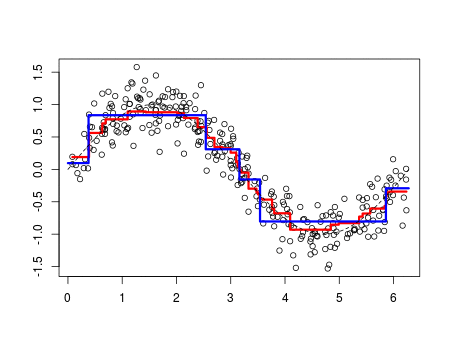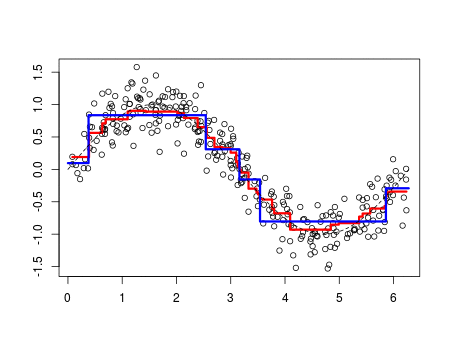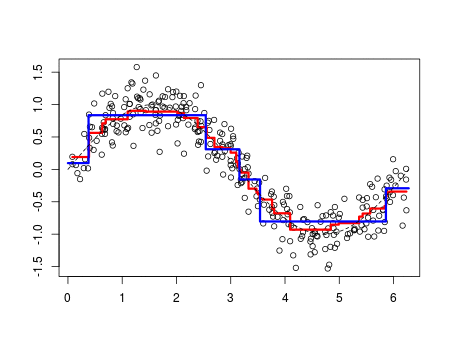
The simple function is a real-valued function $f: \mathrm{X}\to \mathbb{R}$ if and only if it is a finite linear combination of characteristic functions: $$f=\sum_{i=1}^{n}a_k {\chi}{S{k}}$$ where $a_k\in\mathbb{R}$ and the characteristic function is defined as follow $${\chi}{S{k}}=\begin{cases}1, &\text{if $x \in S_{k}$}\ 0, &\text{otherwise}\end{cases}.$$

The tree-based learning algorithms take advantages of these universal approximators to fit the decision function.

The core problem is to find the optimal parameters $a_k\in\mathbb{R}$ and the region $S_k\in\mathbb{R}^p$ when only some finite sample or training data ${(\mathrm{x}^i, y_i)\mid i=1, 2, \dots, n}$ is accessible or available where $\mathrm{x}^i\in\mathbb{R}^p$ and $y_i\in\mathbb{R}$ or some categorical domain and the number of regions also depends on the training data set.

Decision Tree

A decision tree is a set of questions(i.e. if-then sentence) organized in a hierarchical manner and represented graphically as a tree. It use divide-and-conquer strategy recursively as similar as the binary search in the sorting problem. It is easy to scale up to massive data set. The models are obtained by recursively partitioning the data space and fitting a simple prediction model within each partition. As a result, the partitioning can be represented graphically as a decision tree. Visual introduction to machine learning show an visual introduction to decision tree.

In brief, A decision tree is a classifier expressed as a recursive partition of the instance space as a nonparametric statistical method.

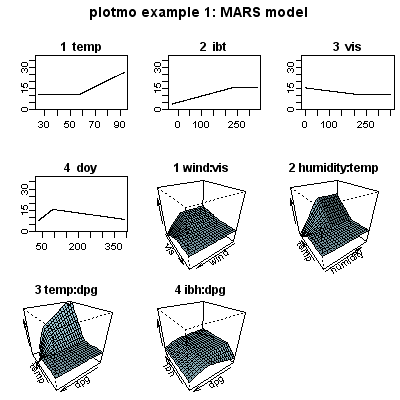
Fifty Years of Classification and Regression Trees and the website of Wei-Yin Loh helps much understand the development of decision tree methods. Multivariate Adaptive Regression Splines(MARS) is the boosting ensemble methods for decision tree algorithms. Recursive partition is a recursive way to construct decision tree.

A Visual and Interactive Guide

Decision tree is represented graphically as a tree as the following.

As shown above, there are differences between the length from root to the terminal nodes, which the inputs arrive at. In another word, some inputs take more tests(pass more nodes) than others. For a given data $(\mathrm x^i, y_i)$ where $\mathrm x^i=(x^i_1, x^i_2, \dots, x^i_p)$. It is obvious that $x^i_1-1<x^i_1< x^i_1+1$ and as binary search, each attribute of the sample can be sorted into some region.

To understand the construction of decision tree, we need to answer three basic questions:

  • What are the contents of the nodes?
  • Why and how is a parent node split into two daughter nodes?
  • When do we declare a terminal node?

The root node contains a sample of subjects from which the tree is grown. Those subjects constitute the so-called learning sample, and the learning sample can be the entire study sample or a subset of it. For example, the root node contains all 3,861 pregnant women who were the study subjects of the Yale Pregnancy Outcome Study. All nodes in the same layer constitute a partition of the root node. The partition becomes finer and finer as the layer gets deeper and deeper. Therefore, every node in a tree is merely a subset of the learning sample.

The core idea of the leaf splitting in decision tree is to decrease the dissimilarities of the samples in the same region, i.e., to produce the terminal nodes that are homogeneous. The goodness of a split must weigh the homogeneities (or the impurities) in the two daughter nodes.

The recursive partitioning process may proceed until the tree is saturated in the sense that the offspring nodes subject to further division cannot be split.

  • there is only one subject in a node.
  • the total number of allowable splits for a node drops as we move from one layer to the next.
  • the number of allowable splits eventually reduces to zero
  • the nodes are terminal when they are not divided further.

The saturated tree is usually too large to be useful.

  • the terminal nodes are so small that we cannot make sensible statistical inference.
  • this level of detail is rarely scientifically interpretable.
  • a minimum size of a node is set a priori.
  • stopping rules
    • Automatic Interaction Detection(AID) (Morgan and Sonquist 1963) declares a terminal node based on the relative merit of its best split to the quality of the root node
  • Breiman et al. (1984, p. 37) argued that depending on the stopping threshold, the partitioning tends to end too soon or too late.

These always bring the side effect - overfitting.

Tree Construction

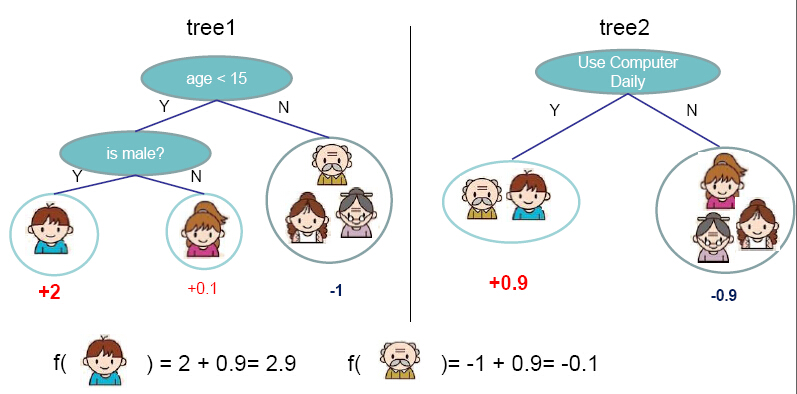
A decision tree is the function $T :\mathbb{R}^d \to \mathbb{R}$ resulting from a learning algorithm applied on training data lying in input space $\mathbb{R}^d$ , which always has the following form: $$ T(x) = \sum_{i\in\text{leaves}} g_i(x)\mathbb{I}(x\in R_i) = \sum_{i\in ,\text{leaves}} g_i(x) \prod_{a\in,\text{ancestors(i)}} \mathbb{I}(S_{a (x)}=c_{a,i}) $$ where $R_i \subset \mathbb{R}^d$ is the region associated with leaf ${i}$ of the tree, $\text{ancestors(i)}$ is the set of ancestors of leaf node $i$, $c_{a,i}$ is the child of node a on the path from $a$ to leaf $i$, and $S_a$ is the n-array split function at node $a$. $g_i(\cdot)$ is the decision function associated with leaf $i$ and is learned only from training examples in $R_i$.

The $g_{i}(x)$ can be a constant in $\mathbb{R}$ or some mathematical expression such as logistic regression. When $g_i(x)$ is constant, the decision tree is actually piecewise constant, a concrete example of simple function.

The interpretation is simple: Starting from the root node, you go to the next nodes and the edges tell you which subsets you are looking at. Once you reach the leaf node, the node tells you the predicted outcome. All the edges are connected by 'AND'.

Template: If feature x is [smaller/bigger] than threshold c AND ??? then the predicted outcome is the mean value of y of the instances in that node.

What is the parameters to learn when constructing a decision tree? The value of leaves $g_i(\cdot)$ and the spliiting function $S_i(\cdot)$. Another approach to depict a decsion tree $T_h = (N_h;L_h)$ is given the set of internal nodes, $N_h$, and the set of leaves, $L_h$.

Algorithm Pseudocode for tree construction by exhaustive search

  1. Start at root node.
  2. For each node ${X}$, find the set ${S}$ that minimizes the sum of the node $\fbox{impurities}$ in the two child nodes and choose the split ${X^{\ast}\in S^{\ast}}$ that gives the minimum overall $X$ and $S$.
  3. If a stopping criterion is reached, exit. Otherwise, apply step 2 to each child node in turn.
Divisive Hierarchical Clustering Decision Tree
From Top to Down From Top to Down
Unsupervised Supervised
Clustering Classification and Regression
Splitting by maximizing the inter-cluster distance Splitting by minimizing the impurities of samples
Distance-based Distribution-based
Evaluation of clustering Accuracy
No Regularization Regularization
No Explicit Optimization Optimal Splitting

Pruning and Regularization

Like other supervised algorithms, decision tree makes a trade-off between over-fitting and under-fitting and how to choose the hyper-parameters of decision tree such as the max depth? The regularization techniques in regression may not suit the tree algorithms such as LASSO.

Pruning is a regularization technique for tree-based algorithm. In arboriculture, the reason to prune tree is because each cut has the potential to change the growth of the tree, no branch should be removed without a reason. Common reasons for pruning are to remove dead branches, to improve form, and to reduce risk. Trees may also be pruned to increase light and air penetration to the inside of the tree’s crown or to the landscape below.

In machine learning, it is to avoid the overfitting, to make a balance between over-fitting and under-fitting and boost the generalization ability. Pruning is to find a subtree of the saturated tree that is most “predictive" of the outcome and least vulnerable to the noise in the data

For a tree $T$ we define $$ R(\mathcal{T})=\sum_{\tau \in \overline{\mathcal{T}}} \boldsymbol{P}{\tau} r(\tau) $$ where $\overline{\mathcal{T}}$ is the set of terminal nodes of $\mathcal T$. $r(\tau)$ measures a certain quality of node $\tau$. It is similar to the sum of the squared residuals in the linear regression. The purpose of pruning is to select the best subtree, $\mathcal T^{\ast}$, of an initially saturated tree, $\mathcal T_0$, such that $R(T )$ is minimized.

The important step of tree pruning is to define a criterion be used to determine the correct final tree size using one of the following methods:

  1. Use a distinct dataset from the training set (called validation set), to evaluate the effect of post-pruning nodes from the tree.
  2. Build the tree by using the training set, then apply a statistical test to estimate whether pruning or expanding a particular node is likely to produce an improvement beyond the training set.
    • Error estimation
    • Significance testing (e.g., Chi-square test)
  3. Minimum Description Length principle : Use an explicit measure of the complexity for encoding the training set and the decision tree, stopping growth of the tree when this encoding size (size(tree) + size(misclassifications(tree)) is minimized.

When the height of a decision tree is limited to 1, i.e., it takes only one test to make every prediction, the tree is called a decision stump. While decision trees are nonlinear classifiers in general, decision stumps are a kind of linear classifiers.

It is also useful to restrict the number of terminal nodes, the height/depth of the decision tree in order to avoid overfitting.

Cost–Complexity

$$R_{\alpha}(\mathcal{T})=R(\mathcal{T})+\alpha|\tilde{\mathcal{T}}|$$

where $\alpha (\geq 0)$ is the complexity parameter and $|\tilde{\mathcal{T}}|$ is the number of terminal nodes in $T$.

The use of tree cost-complexity allows us to construct a sequence of nested “essential subtrees from any given tree T so that we can examine the properties of these subtrees and make a selection from them.

(Breiman et al. 1984, Section 3.3) For any value of the complexity parameter $\alpha$, there is a unique smallest subtree of $T_0$ that minimizes the cost-complexity.

Nested Optimal Subtrees

After pruning the tree using the first threshold, we seek the second threshold complexity parameter, $\alpha_2$. We knew from our previous discussion that $\alpha_2=0.018$ and its optimal subtree is the root-node tree. No more thresholds need to be found from here, because the root-node tree is the smallest one. In general, suppose that we end up with $m$ thresholds, $0<\alpha_1 < \alpha_2\cdots <\alpha_m$.

If $\alpha_1 > \alpha_2$, the optimal subtree corresponding to $\alpha_1$ is a subtree of the optimal subtree corresponding to $\alpha_2$.

We need a good estimate of the misclassification costs of the subtrees. We will select the one with the smallest misclassification cost.

http://support.sas.com/documentation/cdl/en/statug/68162/HTML/default/viewer.htm#statug_hpsplit_details06.htm

Missing values processing

Impact of Missing Data

  • Missing data may lead to serious loss of information.
  • We may end up with imprecise or even false conclusions.
  • Variables change in the selected models.
  • The estimated coefficients can be notably different.

Assuming the features are missing completely at random, there are a number of ways of handling missing data:

  1. Discard observations with any missing values.
  2. Rely on the learning algorithm to deal with missing values in its training phase.
  3. Impute all missing values before training.

For most learning methods, the imputation approach (3) is necessary. The simplest tactic is to impute the missing value with the mean or median of the nonmissing values for that feature. If the features have at least some moderate degree of dependence, one can do better by estimating a predictive model for each feature given the other features and then imputing each missing value by its prediction from the model.

Some software packages handle missing data automatically, although many don’t, so it’s important to be aware if any pre-processing is required by the user.

Surrogate Splits

  • Surrogate splits attempt to utilize the information in other predictors to assist us in splitting when the splitting variable, say, race, is missing.
  • The idea to look for a predictor that is most similar to race in classifying the subjects.
  • One measure of similarity between two splits suggested by Breiman et al. (1984) is the coincidence probability that the two splits send a subject to the same node.

In general, prior information should be incorporated in estimating the coincidence probability when the subjects are not randomly drawn from a general population, such as in case–control studies.

There is no guarantee that surrogate splits improve the predictive power of a particular split as compared to a random split. In such cases, the surrogate splits should be discarded. If surrogate splits are used, the user should take full advantage of them. They may provide alternative tree structures that in principle can have a lower misclassification cost than the final tree, because the final tree is selected in a stepwise manner and is not necessarily a local optimizer in any sense.

Regression Trees

Starting with all of the data, consider a splitting variable $j$ and split point $s$, and define the pair of half-planes $$R_1(j, s)={X\mid X_j\leq s}, R_2(j, s)={X\mid X_j> s}.$$

Then we seek the splitting variable $j$ and split point $s$ that solve $$\min_{j, s}[\min_{c_1}\sum_{x_i\in R_1}(y_i-c_1)^2+\min_{c_2}\sum_{x_i\in R_2}(y_i-c_2)^2].$$

Why the objective function is in squared error rather than others? Maybe it is because of its simplicity to solve.

For any choice $j$ and $s$, the inner minimization is solved by $$\hat{c}{1}=\operatorname{ave}\left(y{i} | x_{i} \in R_{1}(j, s)\right) \text { and } \hat{c}{2}=\operatorname{ave}\left(y{i} | x_{i} \in R_{2}(j, s)\right).$$

For each splitting variable, the determination of the split point $s$ can be done very quickly and hence by scanning through all of the inputs, determination of the best pair $\left(j, s\right)$ is feasible. Having found the best split, we partition the data into the two resulting regions and repeat the splitting process on each of the two regions. Then this process is repeated on all of the resulting regions.

[If you want them to be more robust to outliers, you can try to predict the median of Y|X rather than the mean. But what impurity criterion to use?

Since the median is just the estimator for $Y$ that minimizes the absolute value of the difference: $E(|Y−m|)$, you should choose the split which minimizes the absolute deviation rather than variance. You’ll also want to predict the median, rather than the mean, in each leaf node.

Tree size is a tuning parameter governing the model’s complexity, and the optimal tree size should be adaptively chosen from the data. One approach would be to split tree nodes only if the decrease in sum-of-squares due to the split exceeds some threshold. This strategy is too short-sighted, however, since a seemingly worthless split might lead to a very good split below it.

The preferred strategy is to grow a large tree $T_0$ , stopping the splitting process only when some minimum node size (say 5) is reached. Then this large tree is pruned using cost-complexity pruning.

we define the cost complexity criterion $$C_{\alpha}(T)=\sum_{m=1}^{|T|}N_m Q_m (T) + \alpha |T|.$$

The idea is to find, for each $\alpha$, the subtree $T_{\alpha}\subset T_0$ to minimize $C_{\alpha}(T)$. The tuning parameter $\alpha \geq 0$ governs the tradeoff between tree size and its goodness of fit to the data. Large values of $\alpha$ result in smaller trees $T_{\alpha}$, and conversely for smaller values of $\alpha$. As the notation suggests, with $\alpha = 0$ the solution is the full tree $T_0$.

Classification Trees

If the target is a classification outcome taking values $1,2,\dots,K$, the only changes needed in the tree algorithm pertain to the criteria for splitting nodes and pruning the tree.

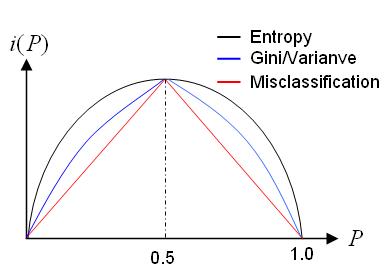
It turns out that most popular splitting criteria can be derived from thinking of decision trees as greedily learning a piecewise-constant, expected-loss-minimizing approximation to the function $f(X)=P(Y=1|X)$. For instance, the split that maximizes information gain is also the split that produces the piecewise-constant model that maximizes the expected log-likelihood of the data. Similarly, the split that minimizes the Gini node impurity criterion is the one that minimizes the Brier score of the resulting model. Variance reduction corresponds to the model that minimizes mean squared error.

Creating a binary decision tree is actually a process of dividing up the input space according to the sum of impurities, which is different from other learning methods such as support vector machine.

  • Intuitively, the least impure node should have only one class of outcome (i.e., $P{Y = 1 | \tau} = 0 \text{ or }1$), and its impurity is zero.
  • Node $\tau$ is most impure when $P{Y = 1 | \tau} =\frac{1}{2}$.
  • The impurity function has a concave shape and can be formally defined as $$i(\tau)=\phi(P(Y=1\mid \tau))$$ where the function $\phi$ has the properties (i) $\phi \geq 0$ and (ii) for any $p \in (0, 1)$, $\phi(p) = \phi(1 - p)$ and $\phi(0) = \phi(1) < \phi(p)$.

C4.5 uses entropy for its impurity function, whereas CART uses a generalization of the binomial variance called the Gini index.

If the training set $D$ is divided into subsets $D_1,\dots, D_k$, the entropy may be reduced, and the amount of the reduction is the information gain,

$$ G(D; D_1, \dots, D_k)=Ent(D)-\sum_{i=1}^{k}\frac{|D_k|}{|D|}Ent(D_k) $$

where $Ent(D)$, the entropy of $D$, is defined as

$$ Ent(D)=\sum_{y \in Y} P(y|D)\log(\frac{1}{P(y | D)}), $$ where $y\in Y$ is the class index.

The information gain ratio of features $A$ with respect of data set $D$ is defined as

$$ g_{R}(D,A)=\frac{G(D,A)}{Ent(D)}. $$ And another option of impurity is Gini index of probability $p$:

$$ Gini(p)=\sum_{y}p_y (1-p_y)=1-\sum_{y}p_y^2. $$

$\color{red}{\text{PS: all above impurities}}$ are based on the probability $\fbox{distribuion}$ of data. So that it is necessary to estimate the probability distribution of each attribute.

Algorithm Splitting Criteria Loss Function
ID3 Information Gain
C4.5 Normalized information gain ratio
CART Gini Index

If your splitting criterion is information gain, this corresponds to a log-likelihood loss function. This works as follows.

If you have a constant approximation $\hat{f}$ to $f$ on some regions $S$, then the approximation that maximizes the expected log-likelihood of the data (that is, the probability of seeing the data if your approximation is correct)is $$L(\hat f) = E(\log P(Y=Y_{observed} | X, f = \hat f)) = \sum_{X_i} Y_i \log \hat f(X_i) + (1 - Y_i) \log (1 - \hat f(X_i))$$ for a binary classification problem where $Y_i \in {0, 1}$ is its classification. Here Suppose $Y$ is determined from $X$ by some function $f(X)=P(Y=1|X)$. First we need to find the constant value $\hat f(X)=f$ that maximizes this value.

Suppose that you have $n$ total instances, $p$ of them positive ($Y=1$) and the rest negative. Suppose that you predict some arbitrary probability $f$ ??? we’ll solve for the one that maximizes expected log-likelihood. So we take the expected log-likelihood $\mathbb E_X(logP(Y=Y_{observed}|X))$, and break up the expectation by the value of $Y_{observed}$:

$$L(\hat f) = (\log P(Y=Y_{observed} | X, Y_{observed}=1)) P(Y_{observed} = 1) \

  • (\log P(Y=Y_{observed} | X, Y_{observed}=0)) P(Y_{observed} = 0)$$

Substituting in some variables gives $$L(\hat f) = \frac{p}{n} \log f

  • \frac{n - p}{n} \log (1 - f).$$

And $\arg\max_{f}L(\hat f)=\frac{p}{n}$ by setting its derivative 0. Let’s substitute this back into the likelihood formula and shuffle some variables around: $$L(\hat f) = \left(f \log f + (1 - f) \log (1 - f) \right).$$

A similar derivation shows that Gini impurity corresponds to a Brier score loss function. The Brier score for a candidate model $$B(\hat f) = E((Y - \hat f(X))^2).$$

Like log-likelihood, the predictions that f^ should make to minimize the Brier score are simply $f=p/n$.

Now let’s take the expected Brier score and break up by $Y$, like we did before: $$B(\hat f) = (1 - \hat f(X))^2 P(Y_{observed} = 1)

  • \hat f(X)^2 P(Y_{observed} = 0)$$ Plugging in some values: $$B(\hat f) = (1 - f)^2 f + f^2(1 - f) = f(1-f)$$ which is exactly (proportional to) the Gini impurity in the 2-class setting. (A similar result holds for multiclass learning as well.)
--- ---
QUEST ?
Oblivious Decision Trees ?
Online Adaptive Decision Trees ?
Lazy Tree ?
Option Tree ?
Oblique Decision Trees ?
MARS ?

Oblique Decision Trees

In this paper, we consider that the instances take the form $(x_1, x_2, \cdots, x_d, c_j)$ , where the $x_i$ are real-valued attributes, and the $c_j$ is a discrete value that represents the class label of the instance. Most tree inducers consider tests of the form $x_i > k$ that are equivalent to axis-parallel hyperplanes in the attribute space. The task of the inducer is to find appropriate values for $i$ and $k$. Oblique decision trees consider more general tests of the form $$\sum_{i=1}^d \alpha_i x_i +\alpha_{d+1}>0$$ where the $\alpha_{d+1}$ are real-valued coefficients

In a compact way, the general linear test can be rewriiten as $$\left<\alpha, x\right>+b>0$$ where $\alpha=(\alpha_1,\cdots, \alpha_d)^T$ and $x=(x_1, x_2, \cdots, x_d)$.

It is natural to generalized to nonlinear test, which can be seen as feature engineering of the input data.

Classification and Regression Tree

Classification and regression trees (CART) are a non-parametric decision tree learning technique that produces either classification or regression trees, depending on whether the dependent variable is categorical or numeric, respectively. CART is both a generic term to describe tree algorithms and also a specific name for Breiman’s original algorithm for constructing classification and regression trees.

https://publichealth.yale.edu/c2s2/8_209304_5_v1.pdf

Incremental Decision Tree

Very Fast Decision Tree

Hoeffding Tree or VFDT is the standard decision tree algorithm for data stream classification. VFDT uses the Hoeffding bound to decide the minimum number of arriving instances to achieve certain level of confidence in splitting the node. This confidence level determines how close the statistics between the attribute chosen by VFDT and the attribute chosen by decision tree for batch learning.

Extremely Fast Decision Tree

Hoeffding Anytime Tree produces the asymptotic batch tree in the limit, is naturally resilient to concept drift, and can be used as a higher accuracy replacement for Hoeffding Tree in most scenarios, at a small additional computational cost.

Although exceedingly simple conceptually, most implementations of tree-based models do not efficiently utilize modern superscalar processors. By laying out data structures in memory in a more cache-conscious fashion, removing branches from the execution flow using a technique called predication, and micro-batching predictions using a technique called vectorization, we are able to better exploit modern processor architectures.

Decision Stream

Decision stream is a statistic-based supervised learning technique that generates a deep directed acyclic graph of decision rules to solve classification and regression tasks. This decision tree based method avoids the problem of data exhaustion in terminal nodes by merging of leaves from the same/different levels of predictive model.

Unlike the classical decision tree approach, this method builds a predictive model with high degree of connectivity by merging statistically indistinguishable nodes at each iteration. The key advantage of decision stream is an efficient usage of every node, taking into account all fruitful feature splits. With the same quantity of nodes, it provides higher depth than decision tree, splitting and merging the data multiple times with different features. The predictive model is growing till no improvements are achievable, considering different data recombinations, and resulting in deep directed acyclic graph, where decision branches are loosely split and merged like natural streams of a waterfall. Decision stream supports generation of extremely deep graph that can consist of hundreds of levels.

Oblivious Decision Trees

Decision Graph

Properties of Decision Tree
Classification and Regression Decision Trees Explained
linearly separable data points.
Limitations of Trees
Tree structure is prone to instability even with minor data perturbations.
To leverage the richness of a data set of massive size, we need to broaden the classic statistical view of “one parsimonious model" for a given data set.
Due to the adaptive nature of the tree construction, theoretical inference based on a tree is usually not feasible. Generating more trees may provide an empirical solution to statistical inference.

Random Forest

YOSHUA BENGIO, OLIVIER DELALLEAU, AND CLARENCE SIMARD demonstrates some theoretical limitations of decision trees. And they can be seriously hurt by the curse of dimensionality in a sense that is a bit different from other nonparametric statistical methods, but most importantly, that they cannot generalize to variations not seen in the training set. This is because a decision tree creates a partition of the input space and needs at least one example in each of the regions associated with a leaf to make a sensible prediction in that region. A better understanding of the fundamental reasons for this limitation suggests that one should use forests or even deeper architectures instead of trees, which provide a form of distributed representation and can generalize to variations not encountered in the training data.

Random forests (Breiman, 2001) is a substantial modification of bagging that builds a large collection of de-correlated trees, and then averages them.

On many problems the performance of random forests is very similar to boosting, and they are simpler to train and tune.

  • For $t=1, 2, \dots, T$:
    • Draw a bootstrap sample $Z^{\ast}$ of size $N$ from the training data.
    • Grow a random-forest tree $T_t$ to the bootstrapped data, by recursively repeating the following steps for each terminal node of the tree, until the minimum node size $n_{min}$ is reached.
      • Select $m$ variables at random from the $p$ variables.
      • Pick the best variable/split-point among the $m$.
      • Split the node into two daughter nodes.
  • Vote for classification and average for regression.

Forest Size

Because of so many trees in a forest, it is impractical to present a forest or interpret a forest. Zhang and Wang (2009): a tree is removed if its removal from the forest has the minimal impact on the overall prediction accuracy

  • Calculate the prediction accuracy of forest $F$, denoted by $p_F$. For every tree, denoted by $T$, in forest $F$, calculate the prediction accuracy of forest $F_{−T}$ that excludes $T$, denoted by $p_{F_{−T}}$.
  • Let $\Delta_{−T}$ be the difference in prediction accuracy between $F$ and $F_{−T} :\Delta_{−T} = p_F ??? p_{F_{−T}}$.
  • The tree $T^p$ with the smallest $\Delta_{−T}$ is the least important one and hence subject to removal: $T^p = \arg\min_{T\in F}( \Delta_{−T})$.

Optimal Size Subforest

properties of random forest
Robustness to Outliers
Scale Tolerance
Ability to Handle Missing Data
Ability to Select Features
Ability to Rank Features

MARS and Bayesian MARS

MARS

Multivariate adaptive regression splines (MARS) provide a convenient approach to capture the nonlinearity aspect of polynomial regression by assessing cutpoints (knots) similar to step functions. The procedure assesses each data point for each predictor as a knot and creates a linear regression model with the candidate feature(s).

Multivariate Adaptive Regression Splines (MARS) is a non-parametric regression method that builds multiple linear regression models across the range of predictor values. It does this by partitioning the data, and run a linear regression model on each different partition.

Whereas polynomial functions impose a global non-linear relationship, step functions break the range of x into bins, and fit a different constant for each bin. This amounts to converting a continuous variable into an ordered categorical variable such that our linear regression function is converted to Equation 1??? $$y_i = \beta_0 + \beta_1 C_1(x_i) + \beta_2 C_2(x_i) + \beta_3 C_3(x_i) \dots + \beta_d C_d(x_i) + \epsilon_i, \tag{1}$$

where $C_n(x)$ represents $x$ values ranging from $% $ for $n=1,2,\dots, d$.

The MARS algorithm builds a model in two steps. First, it creates a collection of so-called basis functions (BF). In this procedure, the range of predictor values is partitioned in several groups. For each group, a separate linear regression is modeled, each with its own slope. The connections between the separate regression lines are called knots. The MARS algorithm automatically searches for the best spots to place the knots. Each knot has a pair of basis functions. These basis functions describe the relationship between the environmental variable and the response. The first basis function is ‘max(0, env var - knot), which means that it takes the maximum value out of two options: 0 or the result of the equation ‘environmental variable value ??? value of the knot???. The second basis function has the opposite form: max(0, knot - env var).

To highlight the progression from recursive partition regression to MARS we start by giving the partition regression model, $$\hat{f}(x)=\sum_{i=1}^{k}a_iB_i(x)\tag{2}$$ where $x\in D$ and $a_i(i=1,2,\dots, k)$ are the suitably chosen coefficients of the basis functions $B_i$ and $k$ is the number of basis functions in the model. These basis functions are such that $B_i(x)=\mathbb{I}(x\in R_i)$ where $\mathbb I$ is the indicator function which is one where the argument is true, zero elsewhere and the $R_i(i=1, \dots, k)$ form a partition of $D$.

The usual MARS model is the same as that given in (2) except that the basis functions are different. Instead the $B_i$ are given by $$B_i(X)=\begin{cases} 1, &\text{$i=1$}\ \Pi_{j=1}^{J_i}[s_{ji}(x_{\nu(ji)}-t_{ji})]{+}, &\text{$i=2,3,\dots$} \end{cases}$$ where ${[\cdot]}{+}=\max(0, \cdot)$; $J_i$ is the degree of the interaction of basis $B_i$, the $s_{ji}$, which we shall call the sign indicators, equal $\pm 1$, $\nu(ji)$ give the index of the predictor variable which is being split on the $t_{ji}$ (known as knot points) give the position of the splits.

Bayesian MARS

A Bayesian approach to multivariate adaptive regression spline (MARS) fitting (Friedman, 1991) is proposed. This takes the form of a probability distribution over the space of possible MARS models which is explored using reversible jump Markov chain Monte Carlo methods (Green, 1995). The generated sample of MARS models produced is shown to have good predictive power when averaged and allows easy interpretation of the relative importance of predictors to the overall fit.

The BMARS basis function can be written as $$B(\vec{x}) = \beta_{0} + \sum_{k=1}^{\mathrm{K}} \beta_{k} \prod_{l=0}^{\mathrm{I}}{\left(x_{l} - t_{k, l}\right)}{+}^{o{k, l}}\tag{1}$$ where $\vec x$ is a vector of input, $t_{k, l}$ is the knot point in the $l^{th}$ dimension of the $k^{th}$ component, the function ${(y)}_{+}$ evaluates to $y$ if $y>0$, else it is 0, $o$ is the polynomial degree in the $l^{th}$ dimension of the $k^{th}$ component, $\beta_k$ is the coefficient of the $k^{th}$ component, $K$ is the maximum number of components of the basis function, and $I$ is the maximum allowed number of interactions between the $L$ dimensions of the input space.

Ensemble methods

There are many competing techniques for solving the problem, and each technique is characterized by choices and meta-parameters: when this flexibility is taken into account, one easily ends up with a very large number of possible models for a given task.

Ensemble methods are meta-algorithms that combine several machine learning techniques into one predictive model in order to decrease variance (bagging), bias (boosting), or improve predictions (stacking).

Bagging Boosting Stacking

Bagging

Bagging, short for 'bootstrap aggregating', is a simple but highly effective ensemble method that creates diverse models on different random bootstrap samples of the original data set. Random forest is the application of bagging to decision tree algorithms.

The basic motivation of parallel ensemble methods is to exploit the independence between the base learners, since the error can be reduced dramatically by combining independent base learners. Bagging adopts the most popular strategies for aggregating the outputs of the base learners, that is, voting for classification and averaging for regression.

  • Draw bootstrap samples $B_1, B_2, \dots, B_n$ independently from the original training data set for base learners;
  • Train the $i$th base learner $F_i$ at the ${B}_{i}$;
  • Vote for classification and average for regression.

It is a sample-based ensemble method.

Random Subspace Methods

Abstract: "Much of previous attention on decision trees focuses on the splitting criteria and optimization of tree sizes. The dilemma between overfitting and achieving maximum accuracy is seldom resolved. A method to construct a decision tree based classifier is proposed that maintains highest accuracy on training data and improves on generalization accuracy as it grows in complexity. The classifier consists of multiple trees constructed systematically by pseudo-randomly selecting subsets of components of the feature vector, that is, trees constructed in randomly chosen subspaces. The subspace method is compared to single-tree classifiers and other forest construction methods by experiments on publicly available datasets, where the method's superiority is demonstrated. We also discuss independence between trees in a forest and relate that to the combined classification accuracy."

Boosting

The term boosting refers to a family of algorithms that are able to convert weak learners to strong learners. It is kind of similar to the "trial and error" scheme: if we know that the learners perform worse at some given data set $S$, the learner may pay more attention to the data drawn from $S$. For the regression problem, of which the output results are continuous, it progressively reduce the error by trial. In another word, we will reduce the error at each iteration.

Methods Overfit-underfitting Training Type
Bagging avoid over-fitting parallel
Boosting avoid under-fitting sequential

AdaBoost

AdaBoost is a boosting methods for supervised classification algorithms, so that the labeled data set is given in the form $D={ (x_i, \mathrm{y}i)}{i=1}^{N}$. AdaBoost is to change the distribution of training data and learn from the shuffled data. It is an iterative trial-and-error in some sense.

Discrete AdaBoost

  • Input $D={ (x_i, \mathrm{y}i)}{i=1}^{N}$ where $x\in \mathcal X$ and $\mathrm{y}\in {+1, -1}$.
  • Initialize the observation weights ${w}_i=\frac{1}{N}, i=1, 2, \dots, N$.
  • For $t = 1, 2, \dots, T$:
    • Fit a classifier $G_t(x)$ to the training data using weights $w_i$.
    • Compute $$err_{t}=\frac{\sum_{i=1}^{N}w_i \mathbb{I}(G_t(x_i) \not= \mathrm{y}i)}{\sum{i=1}^{N} w_i}.$$
    • Compute $\alpha_t = \log(\frac{1-err_t}{err_t})$.
    • Set $w_i\leftarrow w_i\exp[\alpha_t\mathbb{I}(G_t(x_i) \not= \mathrm{y}i)], i=1,2,\dots, N$ and renormalize so that $\sum{i}w_i=1$.
  • Output $G(x)=sign[\sum_{t=1}^{T}\alpha_{t}G_t(x)]$.

The indicator function $\mathbb{I}(x\neq y)$ is defined as $$ \mathbb{I}(x\neq y)= \begin{cases} 1, \text{if $x\neq y$} \ 0, \text{otherwise}. \end{cases} $$

Note that the weight updating $w_i\leftarrow w_i\exp[\alpha_t\mathbb{I}(G_t(x_i) \not= \mathrm{y}_i)]$ so that the weight does not vary if the prediction is correct $\mathbb{I}(G_t(x_i) \not= \mathrm{y}_i)=0$ and the weight does increase if the prediction is wrong $\mathbb{I}(G_t(x_i) \not= \mathrm{y}_i)=1$.

For a two-class problem, an additive logistic model has the form $$\log\frac{P(y=1\mid x)}{P(y=-1\mid x)}=\sum_{m=1}^{M}f_{m}=F(x)$$

where $P(y=-1\mid x)+P(y=1\mid x)=1$; inverting we obtain $$p(x) = P(y=1\mid x) = \frac{\exp(F(x))}{1+\exp(F(x))}.$$

Consider the exponential criterion $$\arg\min_{F(x)}\mathbb{E}[\exp(-yF(x))]\iff F(x)=\frac{1}{2}\log\frac{P(y=1\mid x)}{P(y=-1\mid x)}.$$

The Discrete AdaBoost algorithm (population version) builds an additive logistic regression model via Newton-like updates for minimizing $\mathbb{E}[\exp(-yF(x))]$.

$$ \mathbb{E}[\exp(-yF(x))]=\exp(F(x))P(y=-1\mid x)+\exp(-F(x))P(y=+1\mid x) $$

so that $$ \frac{\partial \mathbb{E}[\exp(-yF(x))]}{\partial F(x)} = - \exp(-F(x))P(y=+1\mid x) + \exp(F(x))P(y=-1\mid x)\tag{1} $$ where and $\mathbb E$ represents expectation. Setting the equation (1) to 0, we get $$F(x)=\frac{1}{2}\log\frac{P(y=1\mid x)}{P(y=-1\mid x)}.$$

So that $$\operatorname{sign}(H(x))=\operatorname{sign}(\frac{1}{2}\log\frac{P(y=1\mid x)}{P(y=-1\mid x)}) \=\begin{cases}1,&\text{if $\frac{P(y=1\mid x)}{P(y=-1\mid x)}>1$}\ -1, &\text{if $\frac{P(y=1\mid x)}{P(y=-1\mid x)}< 1$} \end{cases}=\arg\max_{x\in{+1, -1}}P(f(x)=y\mid x).$$

  • Input $D={ (x_i, \mathrm{y}i)}{i=1}^{N}$ where $x\in \mathcal X$ and $\mathrm{y}\in {+1, -1}$.
  • Initialize the observation weights ${w}_i=\frac{1}{N}, i=1, 2, \dots, N$.
  • For $t = 1, 2, \dots, T$:
    • Fit a classifier $G_t(x)$ to the training data using weights $w_i$.
    • Compute $$err_{t}=\frac{\sum_{i=1}^{N}w_i \mathbb{I}(G_t(x_i) \not= \mathrm{y}i)}{\sum{i=1}^{N} w_i}.$$
    • Compute $\alpha_t = \log(\frac{1-err_t}{err_t})$.
    • Set $w_i\leftarrow w_i\exp[-\alpha_t G_t(x_i)\mathrm{y}i)], i=1,2,\dots, N$ and renormalize so that $\sum{i}w_i=1$.
  • Output $G(x)=sign[\sum_{t=1}^{T}\alpha_{t}G_t(x)]$.

Real AdaBoost

In AdaBoost, the error is binary- it is 0 if the classification is right otherwise it is 1. It is not precise for some setting. The output of decision trees is a class probability estimate $p(x) = P(y=1 | x)$, the probability that ${x}$ is in the positive class

Real AdaBoost

  • Input $D={ (x_i, \mathrm{y}i)}{i=1}^{N}$ where $x\in \mathcal X$ and $y\in {+1, -1}$.
  • Initialize the observation weights ${w}_i=\frac{1}{N}, i=1, 2, \dots, N$;
  • For $m = 1, 2, \dots, M$:
    • Fit a classifier $G_m(x)$ to obtain a class probability estimate $p_m(x)=\hat{P}_{w}(y=1\mid x)\in [0, 1]$, using weights $w_i$.
    • Compute $f_m(x)\leftarrow \frac{1}{2}\log{p_m(x)/(1-p_m(x))}\in\mathbb{R}$.
    • Set $w_i\leftarrow w_i\exp[-y_if_m(x_i)], i=1,2,\dots, N$ and renormalize so that $\sum_{i=1}w_i =1$.
  • Output $G(x)=sign[\sum_{t=1}^{M}\alpha_{t}G_m(x)]$.

The Real AdaBoost algorithm fits an additive logistic regression model by stagewise and approximate optimization of $\mathbb{E}[\exp(-yF(x))]$.

Gentle AdaBoost

  • Input $D={ (x_i, \mathrm{y}i)}{i=1}^{N}$ where $x\in \mathcal X$ and $y\in {+1, -1}$.
  • Initialize the observation weights ${w}_i=\frac{1}{N}, i=1, 2, \dots, N, F(x)=0$;
  • For $m = 1, 2, \dots, M$:
    • Fit a classifier $f_m(x)$ by weighted least-squares of $\mathrm{y}_i$ to $x_i$ with weights $w_i$.
    • Update $F(x)\leftarrow F(x)+f_m (x)$.
    • UPdate $w_i \leftarrow w_i \exp(-\mathrm{y}_i f_m (x_i))$ and renormalize.
  • Output the classifier $sign[F(x)]=sign[\sum_{t=1}^{M}\alpha_{t}f_m(x)]$.

LogitBoost

Given a training data set ${{\mathrm{X}i, y_i}}{i=1}^{N}$, where $\mathrm{X}i\in\mathbb{R}^p$ is the feature and $y_i\in{1, 2, \dots, K}$ is the desired categorical label. The classifier $F$ learned from data is a function $$ F:\mathbb{R}^P\to y \ \quad X_i \mapsto y_i. $$ And the function $F$ is usually in the additive model $F(x)=\sum{m=1}^{M}h(x\mid {\theta}_m)$.

LogitBoost (two classes)

  • Input $D={ (x_i, \mathrm{y}i)}{i=1}^{N}$ where $x\in \mathcal X$ and $y\in {+1, -1}$.
  • Initialize the observation weights ${w}_i=\frac{1}{N}, i=1, 2, \dots, N, F(x)=0, p(x_i)=\frac{1}{2}$;
  • For $m = 1, 2, \dots, M$:
    • Compute the working response and weights: $$z_i = \frac{y_i^{\ast}-p_i}{p_i(1-p_i)},\ w_i = p_i(1-p_i). $$
    • Fit a classifier $f_m(x)$ by weighted least-squares of $\mathrm{y}_i$ to $x_i$ with weights $w_i$.
    • Update $F(x)\leftarrow F(x)+\frac{1}{2}f_m (x)$.
    • UPdate $w_i \leftarrow w_i \exp(-\mathrm{y}_i f_m (x_i))$ and renormalize.
  • Output the classifier $sign[F(x)]=sign[\sum_{t=1}^{M}\alpha_{t}f_m(x)]$.

Here $y^{\ast}$ represents the outcome and $p(y^{\ast}=1)=p(x)=\frac{\exp(F(x))}{\exp(F(x))+\exp(-F(x))}$.

where $r_{i, k}=1$ if $y_i =k$ otherwise 0.

  • LogitBoost used first and second derivatives to construct the trees;
  • LogitBoost was believed to have numerical instability problems.

arc-x4 Algorithm

Recent work has shown that combining multiple versions of unstable classifiers such as trees or neural nets results in reduced test set error. One of the more effective is bagging (Breiman [1996a]) Here, modified training sets are formed by resampling from the original training set, classifiers constructed using these training sets and then combined by voting. Freund and Schapire [1995,1996] propose an algorithm the basis of which is to adaptively resample and combine (hence the acronym--arcing) so that the weights in the resampling are increased for those cases most often misclassified and the combining is done by weighted voting. Arcing is more successful than bagging in test set error reduction. We explore two arcing algorithms, compare them to each other and to bagging, and try to understand how arcing works. We introduce the definitions of bias and variance for a classifier as components of the test set error. Unstable classifiers can have low bias on a large range of data sets. Their problem is high variance. Combining multiple versions either through bagging or arcing reduces variance significantly.

Breiman proposes a boosting algorithm called arc-x4 to investigate whether the success of AdaBoost roots in its technical details or in the resampling scheme it uses. The difference between AdaBoost and arc-x4 is twofold. First, the weight for object $z_j$ at step $k$ is calculated as the proportion of times $z_j$ has been misclassified by the $k - 1$ classifiers built so far. Second, the final decision is made by plurality voting rather than weighted majority voting.

arc represents adaptively resample and combine.

Properties of AdaBoost
AdaBoost is inherently sequential.
The training classification error has to go down exponentially fast if the weighted errors of the component classifiers are strictly better than chance.
A crucial property of AdaBoost is that it almost never overfits the data no matter how many iterations it is run.

Multiclass Boosting

In binary classification we learn a function $f(x)$ which is positive for one class and negative for the other class. This means that $f(x)$ is a transformation that pushes example of the first class toward direction of vector +1 and examples of the other class toward direction of vector -1.

Using this observation, for multiclass boosting, e.g. 3 classes, we need to push examples in three different directions.

multiBoost

Similar to AdaBoost in the two class case, this new algorithm combines weak classifiers and only requires the performance of each weak classifier be better than random guessing (rather than 1/2).

SAMME

  • Initialize the observation weights ${w}_i=\frac{1}{N}, i=1, 2, \dots, N$.
  • For $t = 1, 2, \dots, T$:
    • Fit a classifier $G_t(x)$ to the training data using weights $w_i$.
    • Compute $$err_{t}=\frac{\sum_{i=1}^{N}w_i \mathbb{I}(G_t(x_i) \not= \mathrm{y}i)}{\sum{i=1}^{N} w_i}.$$
    • Compute $\alpha_t = \log(\frac{1-err_t}{err_t})+\log(K-1)$.
    • Set $w_i\leftarrow w_i\exp[\alpha_t\mathbb{I}(G_t(x_i) \not= \mathrm{y}i)], i=1,2,\dots, N$ and renormalize so that $\sum{i}w_i=1$.
  • Output $G(x)=\arg\max_{k}[\sum_{t=1}^{T}\alpha_{t}\mathbb{I}_{G_t(x)=k}]$.

MCBoost

In our paper we showed that for a M-class classification problem, the optimal set of directions will form a simplex in M-1 dimensions. Below you can see examples of those directions for $M = 2, 3, 4$.

Bonsai Boosted Decision Tree

bonsai BDT (BBDT):

  1. $\fbox{discretizes}$ input variables before training which ensures a fast and robust implementation
  2. converts decision trees to n-dimentional table to store
  3. prediction operation takes one reading from this table

The first step of preprocessing data limits where the splits of the data can be made and, in effect, permits the grower of the tree to control and shape its growth; thus, we are calling this a bonsai BDT (BBDT). The discretization works by enforcing that the smallest keep interval that can be created when training the BBDT is: $$\Delta x_{min} > \delta_x \forall x,,\text{on all leaves}$$ where $\delta_x=\min {|x_i-x_j|: x_i, x_j\in x_{discrete}}$.

Discretization means that the data can be thought of as being binned, even though many of the possible bins may not form leaves in the BBDT; thus, there are a finite number, $n^{max}{keep}$, of possible keep regions that can be defined. If the $n^{max}{keep}$ BBDT response values can be stored in memory, then the extremely large number of if/else statements that make up a BDT can be converted into a one-dimensional array of response values. One-dimensional array look-up speeds are extremely fast; they take, in essense, zero time. If there is not enough memory available to store all of the response values, there are a number of simple alternatives that can be used. For example, if the cut value is known then just the list of indices for keep regions could be stored.

Gradient Boosting Decision Tree

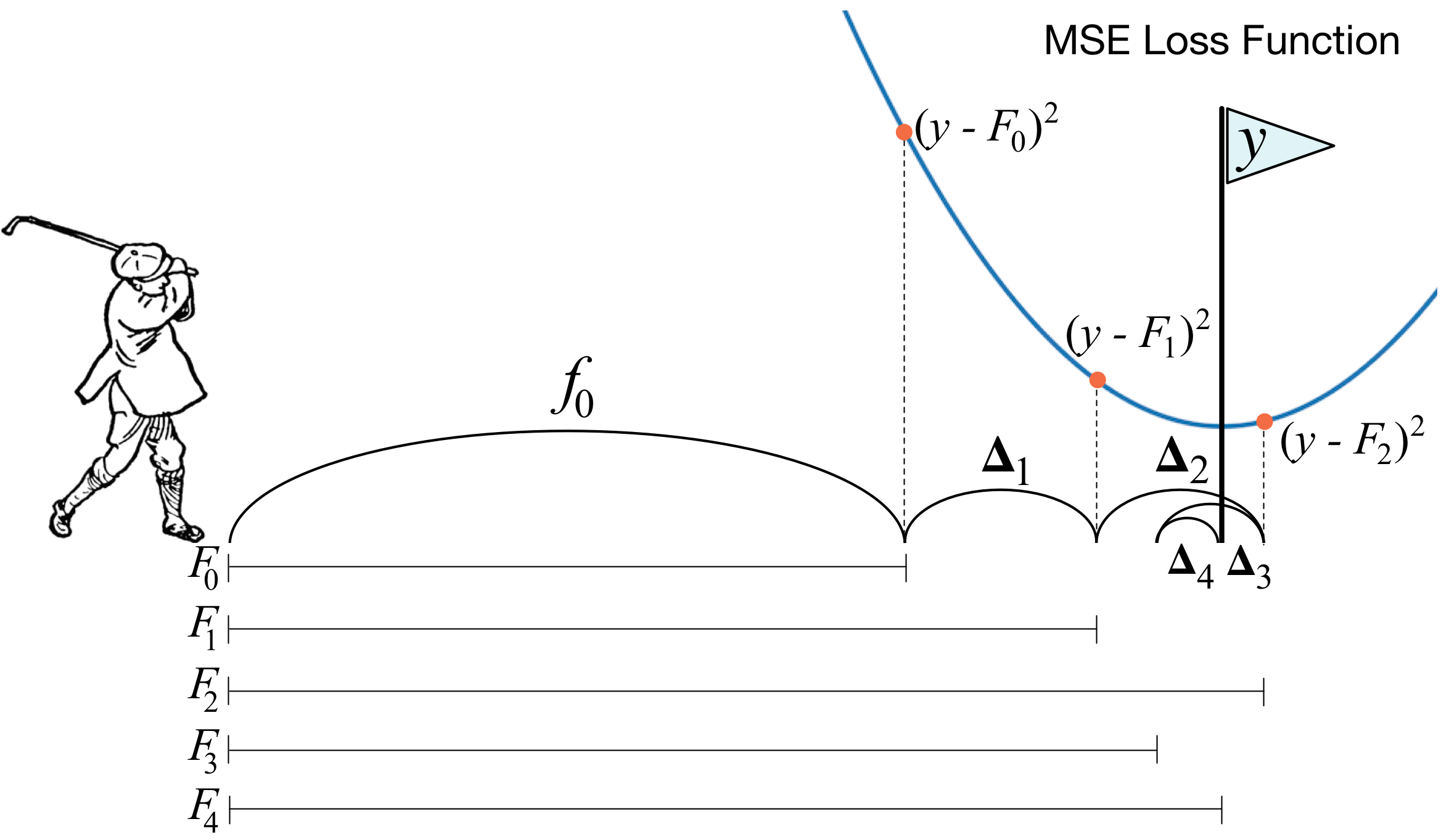
One of the frequently asked questions is What's the basic idea behind gradient boosting? and the answer from [https://explained.ai/gradient-boosting/faq.html] is the best one I know:

Instead of creating a single powerful model, boosting combines multiple simple models into a single composite model. The idea is that, as we introduce more and more simple models, the overall model becomes stronger and stronger. In boosting terminology, the simple models are called weak models or weak learners. To improve its predictions, gradient boosting looks at the difference between its current approximation,$\hat{y}$ , and the known correct target vector ${y}$, which is called the residual, $y-\hat{y}$. It then trains a weak model that maps feature vector ${x}$ to that residual vector. Adding a residual predicted by a weak model to an existing model's approximation nudges the model towards the correct target. Adding lots of these nudges, improves the overall models approximation.

Gradient Boosting

It is the first solution to the question that if weak learner is equivalent to strong learner.

We may consider the generalized additive model, i.e.,

$$ \hat{y}i = \sum{k=1}^{K} f_k(x_i) $$

where ${f_k}_{k=1}^{K}$ is regression decision tree rather than polynomial. The objective function is given by

$$ obj = \underbrace{\sum_{i=1}^{n} L(y_i,\hat{y}i)}{\text{error term} } + \underbrace{\sum_{k=1}^{K} \Omega(f_k)}_{regularazation} $$

where $\sum_{k=1}^{K} \Omega(f_k)$ is the regular term.

The additive training is to train the regression tree sequentially. The objective function of the $t$th regression tree is defined as

$$ obj^{(t)} = \sum_{i=1}^{n} L(y_i,\hat{y}^{(t)}i) + \sum{k=1}^{t} \Omega(f_k) \ = \sum_{i=1}^{n} L(y_i,\hat{y}^{(t-1)}_i + f_t(x_i)) + \Omega(f_t) + C $$

where $C=\sum_{k=1}^{t-1} \Omega(f_k)$.

Particularly, we take $L(x,y)=(x-y)^2$, and the objective function is given by

$$ obj^{(t)} = \sum_{i=1}^{n} [y_i - (\hat{y}^{(t-1)}i + f_t(x_i))]^2 + \Omega(f_t) + C \ = \sum{i=1}^{n} [-2(y_i - \hat{y}^{(t-1)}_i) f_t(x_i) + f_t^2(x_i) ] + \Omega(f_t) + C^{\prime} $$

where $C^{\prime}=\sum_{i=1}^{n} (y_i - \hat{y}^{(t-1)}i)^2 + \sum{k=1}^{t-1} \Omega(f_k)$.

If there is no regular term $\sum_{k=1}^{t} \Omega(f_k)$, the problem is simplified to $$\arg\min_{f_{t}}\sum_{i=1}^{n} [-2(y_i - \hat{y}^{(t-1)}_i) f_t(x_i) + f_t^2(x_i) ]\implies f_t(x_i) = (y_i - \hat{y}^{(t-1)}_i) $$ where $i\in {1,\cdots, n}$ and $(y_i - \hat{y}^{(t-1)}i)=- \frac{1}{2}{[\frac{\partial L(\mathrm{y}i, f(x_i))}{\partial f(x_i)}]}{f=f{t-1}}$.

Boosting for Regression Tree

  • Input training data set ${(x_i, \mathrm{y}_i)\mid i=1, \cdots, n}, x_i\in\mathcal x\subset\mathbb{R}^n, y_i\in\mathcal Y\subset\mathbb R$.
  • Initialize $f_0(x)=0$.
  • For $t = 1, 2, \dots, T$:
    • For $i = 1, 2,\dots , n$ compute the residuals $$r_{i,t}=y_i-f_{t-1}(x_i)=y_i - \hat{y}_i^{t-1}.$$
    • Fit a regression tree to the targets $r_{i,t}$ giving terminal regions $$R_{j,m}, j = 1, 2,\dots , J_m. $$
    • For $j = 1, 2,\dots , J_m$ compute $$\fbox{$\gamma_{j,t}=\arg\min_{\gamma}\sum_{x_i\in R_{j,m}}{L(\mathrm{d}i, f{t-1}(x_i)+\gamma)} $}. $$
    • Update $f_t = f_{t-1}+ \nu{\sum}{j=1}^{J_m}{\gamma}{j, t} \mathbb{I}(x\in R_{j, m}),\nu\in(0, 1)$.
  • Output $f_T(x)$.

For general loss function, it is more common that $(y_i - \hat{y}^{(t-1)}i) \not=-\frac{1}{2} {[\frac{\partial L(\mathrm{y}i, f(x_i))}{\partial f(x_i)}]}{f=f{t-1}}$.

Gradient Boosting for Regression Tree

  • Input training data set ${(x_i, \mathrm{y}_i)\mid i=1, \cdots, n}, x_i\in\mathcal x\subset\mathbb{R}^n, y_i\in\mathcal Y\subset\mathbb R$.
  • Initialize $f_0(x)=\arg\min_{\gamma} L(\mathrm{y}_i,\gamma)$.
  • For $t = 1, 2, \dots, T$:
    • For $i = 1, 2,\dots , n$ compute $$r_{i,t}=-{[\frac{\partial L(\mathrm{y}i, f(x_i))}{\partial f(x_i)}]}{f=f_{t-1}}.$$
    • Fit a regression tree to the targets $r_{i,t}$ giving terminal regions $$R_{j,m}, j = 1, 2,\dots , J_m. $$
    • For $j = 1, 2,\dots , J_m$ compute $$\gamma_{j,t}=\arg\min_{\gamma}\sum_{x_i\in R_{j,m}}{L(\mathrm{d}i, f{t-1}(x_i)+\gamma)}. $$
    • Update $f_t = f_{t-1}+ \nu{\sum}{j=1}^{J_m}{\gamma}{j, t} \mathbb{I}(x\in R_{j, m}),\nu\in(0, 1)$.
  • Output $f_T(x)$.

An important part of gradient boosting method is regularization by shrinkage which consists in modifying the update rule as follows: $$ f_{t} =f_{t-1}+\nu \underbrace{ \sum_{j = 1}^{J_{m}} \gamma_{j, t} \mathbb{I}(x\in R_{j, m}) }{ \text{ to fit the gradient} }, \ \approx f{t-1} + \nu \underbrace{ {\sum}{i=1}^{n} -{[\frac{\partial L(\mathrm{y}i, f(x_i))}{\partial f(x_i)}]}{f=f{t-1}} }_{ \text{fitted by a regression tree} }, \nu\in(0,1). $$

Note that the incremental tree is approximate to the negative gradient of the loss function, i.e., $$\fbox{ $\sum_{j=1}^{J_m} \gamma_{j, t} \mathbb{I}(x\in R_{j, m}) \approx {\sum}{i=1}^{n} -{[\frac{\partial L(\mathrm{y}i, f(x_i))}{\partial f(x_i)}]}{f=f{t-1}}$ }$$ where $J_m$ is the number of the terminal regions and ${n}$ is the number of training samples/data.

Method | Hypothesis space| Update formulea | Loss function ---|---|---|---|--- Gradient Descent | parameter space $\Theta$ | $\theta_t=\theta_{t-1}-\rho_t\underbrace{\nabla_{\theta} L\mid_{\theta=\theta_{t-1}}}{\text{Computed by Back-Propagation}}$ |$L(f)=\sum{i}\ell(y_i, f(x_i\mid \theta))$ Gradient Boost | function space $\mathcal F$ | $F_{t}= F_{t-1}- \rho_t\underbrace{\nabla_{F} L\mid_{F=F_{t-1}}}{\text{Approximated by Decision Tree}}$ | $L(F)=\sum{i}\ell(y_i, F(x_i))$

Ensemble Methods Training Data Decision Tree Construction Update Formula
AdaBoost $(x_i, y_i, w_{i, t})$ Fit a classifier $G_t(x)$ to the training data using weights $w_i$ $f_t=f_{t-1}+\alpha_t G_t$
Gradient Boost $(x_i, y_i, r_{i, t})$ Fit a tree $G_t(x)$ to the targets $r_{i,t}$ $f_t=f_{t-1}+\nu G_t$.

Note that $\alpha_t$ is computed as $\alpha_t=\log(\frac{1-err_t}{err_t})$ while the shrinkage parameter $\nu$ is chosen in $(0, 1)$. AdaBoost is desined for any classifier while Gradient Boost methods is usually applied to decision tree.

Stochastic Gradient Boost

A minor modification was made to gradient boosting to incorporate randomness as an integral part of the procedure. Specially, at each iteration a subsample of the training data is drawn at random (without replacement) from the full training data set. This randomly selected subsamples is then used, instead of the full sample, to fit the base learner and compute the model update for the current iteration.

Stochastic Gradient Boosting for Regression Tree

  • Input training data set ${(x_i, \mathrm{y}i)\mid i=1, \cdots, n}, x_i\in\mathcal x\subset\mathbb{R}^n, y_i\in\mathcal Y\subset\mathbb R$. Amd ${{\pi(i)}}1^N$ be a random permutation of their integers ${1,\dots, n}$. Then a random sample of size $\hat n< n$ is given by ${(x{\pi(i)}, \mathrm{y}{\pi(i)})\mid i=1, \cdots, \hat n}$.
  • Initialize $f_0(x)=\arg\min_{\gamma} L(\mathrm{y}_i,\gamma)$.
  • For $t = 1, 2, \dots, T$:
    • For $i = 1, 2,\dots , \hat n$ compute $$r_{\pi(i),t}=-{[\frac{\partial L(\mathrm{y}{\pi(i),t}, f(x{\pi(i),t}))}{\partial f(x_{\pi(i),t})}]}{f=f{t-1}}.$$
    • Fit a regression tree to the targets $r_{\pi(i),t}$ giving terminal regions $$R_{j,m}, j = 1, 2,\dots , J_m. $$
    • For $j = 1, 2,\dots , J_m$ compute $$\gamma_{j,t}=\arg\min_{\gamma}\sum_{x_{\pi(i)}\in R_{j,m}}{L(\mathrm{d}i, f{t-1}(x_{\pi(i)})+\gamma)}. $$
    • Update $f_t = f_{t-1}+ \nu{\sum}{j=1}^{J_m}{\gamma}{j, t} \mathbb{I}(x\in R_{j, m}),\nu\in(0, 1)$.
  • Output $f_T(x)$.

xGBoost

In Gradient Boost, we compute and fit a regression a tree to $$ r_{i,t}=-{ [\frac{\partial L(\mathrm{d}i, f(x_i))}{\partial f(x_i)}] }{f=f_{t-1}}. $$ Why not the error $L(\mathrm{d}_i, f(x_i))$ itself? Recall the Taylor expansion as following $$f(x+h) = f(x)+f^{\prime}(x)h + f^{(2)}(x)h^{2}/2!+ \cdots +f^{(n)}(x)h^{(n)}/n!+\cdots$$ so that the non-convex error function can be expressed as a polynomial in terms of $h$, which is easier to fit than a general common non-convex function. So that we can implement additive training to boost the supervised algorithm.

In general, we can expand the objective function at $x^{t-1}$ up to the second order

$$ obj^{(t)} = \sum_{i=1}^{n} L[y_i,\hat{y}^{(t-1)}i + f_t(x_i)] + \Omega(f_t) + C \ \simeq \sum{i=1}^{n} \underbrace{ [L(y_i,\hat{y}^{(t-1)}_i) + g_i f_t(x_i) + \frac{h_i f_t^2(x_i)}{2}